Conséquence du graphe fermé
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
melreg
- Membre Relatif
- Messages: 325
- Enregistré le: 10 Déc 2007, 20:09
-
par melreg » 20 Nov 2008, 11:46
Bonjour,
Il paraît qu'une conséquence du théorème du graphe fermé (c.f.
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_du_graphe_ferm%C3%A9 ) est que si E et F sont deux espaces de Banach, f une application linéaire continue de (E,
) dans F, alors f est encore continue de (E*,
*) dans F où E*
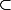
E et
* est une topologie moins fine que
... c'est vrai?
Je désire l'appliquer à l'espace de Sobolev d'ordre 1
)
et à
)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 20 Nov 2008, 19:30
Ça parait étrange ... surtout si on prend E=E*=F et f=Id, ça voudrait pas dire que toute topologie moins fine est équivalente à sa grande soeur ou j'dis n'imp comme d'hab ?
-
melreg
- Membre Relatif
- Messages: 325
- Enregistré le: 10 Déc 2007, 20:09
-
par melreg » 21 Nov 2008, 16:42
Oui bizarre... je vais revoir tout ça!
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 21 Nov 2008, 23:01
Tiens nous au courant !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
