Connexité !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 17:33
par barbu23 » 09 Nov 2007, 17:33
Bonjour :
Définition :
est une espace topologique quelconque.

est connexe si et seulement si une des propriétés suivantes est verifiée :


ne peut s'ecrire comme reunion disjoints de deux ouverts non vides.
 $)

ne peut s'écrire comme reunion disjoints de deux fermés non vides.
 $)
les seules parties à la fois ouvertes et fermés sont

et

.
Theorème :L'image d'un connexe par une application continue est connexe.
Preuve :
connexe.
 $)
. (

est continue ).
Soit

une partie de

qui est à la fois ouverte et fermé.

 $)
est ouvert et fermé de

qui est connexe.
Donc :
 = \{ \empty \\ ou \\ A $)
Donc :
) = F = \{ f(\empty) = \empty \\ ou \\ f(A) = B $)
.
Donc

est connexe.
Questions : $)
Pourquoi
) = F $)
( En fait :
) \subset F $)
est clair )... mais pour
) $)
, je ne sais pas encore pourquoi .. ! Est ce que vous pouvez m'aider ?!
Merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Nov 2007, 17:43
par tize » 09 Nov 2007, 17:43
Bonsoir,
ça parait clair, si x est dans F et z dans f^(-1)({x})={y de A; f(y)=x} alors f(z)=x par définition ! Donc F est inclus dans f(f^(-1)(F)).
 par marie-josèphe » 09 Nov 2007, 17:44
par marie-josèphe » 09 Nov 2007, 17:44
bjr,
F n'est pas seulement un sous-ensemble de l'espace d'arrivée mais une partie de
f(A).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 17:55
par barbu23 » 09 Nov 2007, 17:55
D'accord, merci beaucoup à vous deux !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 19:29
par barbu23 » 09 Nov 2007, 19:29
Bonsoir :
Soir

une partie convexe de
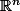
.
Alors :

est connexe.

.

est connexe.
En effet :
Car :
 = M + t . (N-M) $)
.
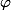
est continue et

est connexe.
Donc :

Ensuite le prof écrit :



est connexe.
Alors , pouvez vous m'expliquer quelle propriété le prof a utilisé ? Tout ce qu'on a étudié en cours.. c'est que la reunion de connexes est connexe que si l'intersection de ses connexes est non vide ! mais l'intersection ici est vide car il n'existe aucun point de

qui appartient à tous les segments de

.
Merci d'avance de votre aide !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 19:54
par barbu23 » 09 Nov 2007, 19:54
Help pls !! :cry:
Merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Nov 2007, 20:50
par tize » 09 Nov 2007, 20:50
Bonsoir,
quel est ton problème exactement, c'est ça :

?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 20:57
par barbu23 » 09 Nov 2007, 20:57
oui, je sais pas comment le prof a conclu qu'à partir de cette reunion que tu viens d'ecrire "tize", que

est connexe !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Nov 2007, 21:01
par tize » 09 Nov 2007, 21:01
En fait il est plus normal de considérer :

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 21:06
par barbu23 » 09 Nov 2007, 21:06
oui, ça je sais, mais tu peux m'expliquer pourquoi cet ensemble est connexe ?!
Merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Nov 2007, 21:09
par tize » 09 Nov 2007, 21:09
pour tout N dans A :

est connexe.

donc A est connexe...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 21:24
par barbu23 » 09 Nov 2007, 21:24
oué, mais c'est pas ça ce qu'il faut avoir , non ?
Il faut que :

, pour tout

et pas pour

fixé .. ! ici ce n'est pas le cas

!! :triste:
Il y'a un autre resultat que j'ai trouvé sur wikipedia, mais le prof nous l'a pas enseigné ! c'est que si
_{n \in \mathcal{N}} $)
une suite de connexes tel que :


... alors la reunion des

est connexe !! ça peut aider à montrer que

est connexe !! Malheureusement, on l'a pas fait en classe !! mais jusqu'à maintenant, j'arrive pas à comprendre la methode du prof !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2007, 22:06
par barbu23 » 09 Nov 2007, 22:06
Help pls !! :doh: :cry:
Merci d'avance !!
 par legeniedesalpages » 09 Nov 2007, 22:34
par legeniedesalpages » 09 Nov 2007, 22:34
Salut, en reformulant ce que t'as déjà dit Tize,
Si A est non vide, tu considères un point
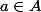
.
Soit

la famille des segments contenus dans A et qui contiennent

.
1) Vérifier qu'on a bien
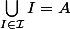
à l'aide de la définition de la convexité;
2) Vérifier que les éléments de

sont connexes (ce qu' a déjà fait ton prof dans sa preuve);
3) Comme les éléments de

sont connexes et ont l'élément

en commun (donc d'intersection non vide), A est connexe.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 10:38
par barbu23 » 10 Nov 2007, 10:38
Bonjour "legeniedesalpages" :
legeniedesalpages a écrit:1) Vérifier qu'on a bien
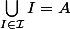
à l'aide de la définition de la convexité;
c'est ça le problème ? il n'y'a pas :
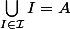
... tous les segments passe par

non , je ne crois pas !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 10:56
par barbu23 » 10 Nov 2007, 10:56
Bonjour :
Théorème :Soit

une partie d'un espace topologique

telle que :

.
Alors

est connexe.
Preuve :Supposons que

avec :

et

fermés de

non vides disjoints.

et

avec :

et

deux fermés de

.


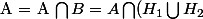 = ( A \bigcap H_{1} ) \bigcap ( A \bigcap H_{2} ) = ( A \bigcap F_{1} ) \bigcap ( A \bigcap F_{2} ) $)

et

sont deux fermés de

disjoints.
Puisque

est connexe , alors :

ou

.
Par exemple :





fermé.


.


et

.
Donc

est connexe.
Questions : $)
Comment on est passé de

à

et

.
Merci d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 11:29
par barbu23 » 10 Nov 2007, 11:29
Bonjour :


est une espace topologique connexe si et seulement une de ses conditions et équivalentes :
 $)
les seules parties à la fois ouvertes et fermés sont

et

.
 $)

ne peut s'écrire comme réunion disjoints de deux fermés non vides.
Preuve : \Longrightarrow 2) $)
Supposons

avec :

et

deux ouverts non vides tel que :

.

^{c} = W_{2} $)
est à la fois ouvert et fermé.


ou

( contradiction ).
Par conséquent :

ne peut s"écrire comme réunion disjints de deux ouverts non vides .
Questions : $)
Pourquoi, il y'a contradiction dans la demonstration !! je vois pas encore pourquoi !! :lol2:
Merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 10 Nov 2007, 11:46
par tize » 10 Nov 2007, 11:46
Bonjour,

donc

et

or

donc
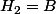
et en particulier

.
Mais puisque

avec
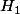
et
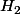
d'intersection vide alors nécessairement

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 11:53
par barbu23 » 10 Nov 2007, 11:53
Merci beaucoup "tize" !! :lol2:
Et pour l'autre question : "contradiction" ?
Merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 10 Nov 2007, 11:58
par tize » 10 Nov 2007, 11:58
barbu23 a écrit:Bonjour :


est une espace
topologique si et seulement une de ses conditions
et équivalentes :
???? tu n'as pas oublié quelque chose...genre connexe ...
barbu23 a écrit:...Supposons

avec :

et

deux ouverts non vides tel que :

.

???
barbu23 a écrit:
ou

( contradiction ).
Il y a contradiction car

et

sont deux ouverts
non vides donc nécessairement

mais dans ce cas c'est

car

or c'est impossible.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
est une espace topologique si et seulement une de ses conditions et équivalentes :
avec :
et
deux ouverts non vides tel que :
.
ou
( contradiction ).