Connexité par arc

par **Nightmare** » 25 Nov 2009, 20:00

Salut à tous :happy3:

Question rapide : Si on retire une partie dénombrable d'une boule fermée de

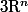
est elle encore connexe par arc ? Quid d'une boule ouverte ?

Ajout : Quid d'un ouvert connexe quelconque ? :lol3:

Bonne réflexion.

:happy3:

par **Doraki** » 25 Nov 2009, 20:09

Je crois bien que dans les deux cas,
En prenant 2 points A et B de la boule (sans trous et pour n>=2) on a une infinité non dénombrable de chemins dans la boule allant de A à B, qui sont deux à deux disjoints en excluant A et B.
Et quand on a ça c'est pas avec une infinité dénombrable de trous qu'on va éliminer tous les chemins.

Quant aux ouverts quelconques, on peut toujours recouvrir un chemin de A à B par un collier de petites sphères.

par **Nightmare** » 25 Nov 2009, 20:15

C'est effectivement vrai dans tous les cas mais ce n'est pas trivial bien qu'à priori ça paraisse intuitif. Cela dit j'ai réussi à le montrer que les boules mais par pour un (ouvert) connexe quelconque.

par **Nightmare** » 25 Nov 2009, 20:17

Je ne crois pas que ce soit vrai pour un ouvert quelconque en fait.

par **Nightmare** » 25 Nov 2009, 20:18

Enfin, c'est même sur si on prend par exemple une réunion disjointe de deux boules ouvertes.

Bref, cela dit pour un ouvert connexe effectivement la construction en collier à l'air de marcher mais n'est pas facile à écrire.

par **ffpower** » 25 Nov 2009, 20:19

deja,dans le 2-ieme cas(qui implique je pense le premier) ainsi que la question ajoutee, on a un ouvert,donc connexe par arc<=>connexe
ce qui peut simplifier la question. Dans le cas d une boule de R^n, on peut formaliser l idee de Doraki et montrer par des arguments de cardinalité que l on peut relier 2 points par un chemin affine par morceau ( et n ayant en fait que 2 morceaux )
ceci ne marche evidemment pas avec R,et pour le cas général,il faut donc a priori plus d hypotheses

par **Nightmare** » 25 Nov 2009, 20:22

Oui c'est à peu près ce que j'ai fait, c'est bizarre car comme le remarque Doraki ça semble intuitivement simple mais j'ai l'impression que mes preuves sont bizarrement longues.

par **Nightmare** » 25 Nov 2009, 20:22

Au passage, il me semble que c'est vrai en remplaçant R^n par n'importe quelle variété topologique, à vérifier.

par **ffpower** » 25 Nov 2009, 20:23

pour un ouvert quelconque de R^n, c est le meme procédé. On montre par connexité que 2 points peuvent etre relié par un chemin affine par morceaux,puis on perturbe les sommets de ce chemin pour obtenir un nouveau chemin affine par morceaux qui esquive les points souhaités..

par **ffpower** » 25 Nov 2009, 20:27

la preuve n est pas longue.Dans le cas de la boule:soit A et B 2 points fixés,et M se balladant sur la mediatrice de AB inter la boule. les chemins du type AMB sont tous disjoints, et comme y en a un nb indénombrable, l un d eux esquivent tous les points qu on a viré..

ps:on est pas obligé de prendre la mediatrice,n importe qu elle droite non parallele a (AB) fait l affaire..

par **Nightmare** » 25 Nov 2009, 22:40

ffpower a écrit:la preuve n est pas longue.Dans le cas de la boule:soit A et B 2 points fixés,et M se balladant sur la mediatrice de AB inter la boule. les chemins du type AMB sont tous disjoints, et comme y en a un nb indénombrable, l un d eux esquivent tous les points qu on a viré..

ps:on est pas obligé de prendre la mediatrice,n importe qu elle droite non parallele a (AB) fait l affaire..

On est d'accord, c'est ce que j'ai fait. Je dis que c'est long car finalement la formalisation est assez longue à rédiger rigoureusement.

Connexité par arc

Connexité par arc

Qui est en ligne