Connexité locale

[legeniedesalpages]

Bonjour,

je bloque sur cette question:

Montrer que si est localement connexe et si est ouvert et fermé, alors est réunion de composantes connexes.

Alors je sais que dans un espace localement connexe, les composantes connexes sont ouvertes et fermées, mais je ne vois pas comment résoudre cette question, enfin surtout pour l'inclusion .

Merci pour votre aide.

[mathelot]

:

Montrer que si est localement connexe et si est ouvert et fermé, alors est réunion de composantes connexes.

je pense que c'est faux:

[legeniedesalpages]

je pense que c'est faux:

une union vide donne l'ensemble vide, vu que est un monoïde d'élément neutre on peut réfugier ce cas à l'aide de la convention classique.

[barbu23]

Bonjour "legeniedesalpages" :
J'ai pas la reponse à ta question pour le moment, néanmoins je crois que je suis sur la bonne voix avec le petit raisonnement que je vais t'avancer dans ce qui suit :
est un espace topologique localement connexe et
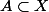
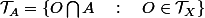
On munit de la topologie trace ( Topologie induite de la topologie ) : et on obtient ainsi : comme espace topologique qui est un sous espace de .
est, par hypothèse, à la fois ouvert et fermé ( pour la topologie induite biensûr ) ... Donc : est un espace topologique connexe ...
Alors, il reste à montrer la validité de ta proposition !
Generalement, quant l'espace est connexe, pas besoin d'evoquer les composantes connexes ... par contre, quant l'espace est localement connexe ( ce qui est le cas ici pour ), on travaille avec les composantes connexes qui remplacent la notion de connexe ... !
Et donc, puisque ici est connexe, est connexe ( un seul morceau : ) ... Si n'etait pas connexe , alors : est une partition deux à deux disjointes de connexes ... !
Ben, voilà, j'espère que ça va t'aider pour trouver le resultat final de ta proposition ... !
Je pense qu'on est tout proche de la fin du problème ... !
Donc : puisque est connexe, ( qui est un connexe contenant ... un seul morceau : ) Il faut montrer à mon avis que son intersection avec le complementaire de est ou quelque chose comme ça ... !
Cordialement ... !

[barbu23]

Par absurde, si on suppose que l'intersection avec est non vide celà veut dire que son reunion avec qui est egale à tout entier est connexe ... Or : n'est pas connexe mais, localement connexe ... Donc, on aboutit à une contradiction ... ! Donc : c'est egale à ... !
Cordialement ... !

[barbu23]

Voilà, donc le bilan qu'on peut faire à la fin comme conclusion: on essaye de dechiffrer les données, et comprendre la structure de ta proposition ... ! Si on comprends la structure de ta proposition, on comprendra comment la resoudre ... ! C'est comme dans une carte ( geographique ... ) si on la comprenne dans son ensemble, on comprendra comme aller d'un coin à l'autre sur cette carte ... ! la même chose ici ... ! :zen:
Cordialement ... !

[ThSQ]

Trop simple pour être correct ?? :



A et B sont ouverts et fermés et disjoints donc l'un est vide.

[mathelot]

est, par hypothèse, à la fois ouvert et fermé ( pour la topologie induite biensûr ) ... Donc : est un espace topologique connexe ...

est ouvert et fermé pour la topologie induite et n'est pas connexe.

De manière très générale, si un espace a plus d'une composante connexe,
il n'est pas connexe.

D'autre part, un espace connexe peut ne pas être localement connexe
(on considère la famille des demi-droites horizontales du plan, d'ordonnées
rationnelles, d'équation et que l'on raccorde via l'axe y'oy)
et évidemment un espace localement connexe n'est pas nécessairement connexe.

Un espace peut être localement connexe sans être localement connexe par arcs (adhérence du graphe de )

[legeniedesalpages]

D'autre part, un espace connexe peut ne pas être localement connexe

ça me semble faux.

Si on considère un espace connexe . Soit un point de , est un voisinage connexe de .

[legeniedesalpages]

Trop simple pour être correct ?? :



A et B sont ouverts et fermés et disjoints donc l'un est vide.

ah oui j'y vois un peu mieux.

merci

[mathelot]

ça me semble faux.

Si on considère un espace connexe . Soit un point de , est un voisinage connexe de .

ça ne suffit pas que E soit connexe. Il faut qu'en tout point,
il y ait une base de voisinages connexes.

[legeniedesalpages]

ah oui autant pour moi :lol2:, la définition est plus forte que je pensais,
je croyais naïvement que c'était du même moule que "localement compact",

merci.