Connexion affine non métrisable?

[Aristarque]

Je cherche un exemple de variété à connexion affine qui ne serait
pas métrisable, c'est-à-dire qui ne puisse être muni d'une forme
quadratique différentielle pour en faire un espace de Riemann
tel que la connexion soit adapté à la métrique.

ESt-ce que cela existe?

Y a t il des propriétés affines simples qu'auraient les espaces à connexion affines métrisables et pas les autres?

[mathelot]

Bonsoir,

ce n'est pas évident.
j'ai pensé au truc suivant : il y a le paradoxe de Banach-Tarski .
On découpe une sphère en une infinité de morceaux, il y a une étape de
la découpe où les morceaux ne sont pas mesurables et on recolle ensuite...
en deux sphères isométriques à la 1ère.

Si on essayait de transporter la structure ,par bijection ensembliste,
d'une sphère sur les deux sphères ? peut être que, formellement,
les axiomes seraient conservés à cause du caractère bijectif.

[Aristarque]

Merci Mathelot pour ta réponse mais il me semble qu'il y a une confusion.
Le paradoxe de Banach-Tarski est un paradoxe sur la notion de "mesurabilité"
de la théorie de la mesure, la mesure de Lebesgue par exemple. Il me semble
que cela n'a pas grand chose à voir avec la "métrisabilité" au sens où je l'ai définie non?

[mathelot]

Bon, j'essaye de répondre à la question comme je peux.

1ère idée
Concernant une surface ou une variété de Riemann, les changements de cartes sont holomorphes. Un moyen simple que ça ne soient pas une variété de Riemann, c'est que les changements de cartes soient anti-holomorphes ?
ie, fonction des coordonnées ?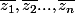

2ème idée
maintenant autre point, pour construire du "topologique pas métrisable", il faut aller voir dans les espaces topologiques plus généraux (je me souviens de résultat du style: les ensembles de fonctions réelles munis de la topologie de la convergence simple ne sont pas métrisables)
après, si on arrive à construire une forme quadratique en tout point
(= pour toute fonction) ça serait bien. Peut être un carré d'une masse de Dirac, pourquoi pas ?
bon, essayons un carré de masse de Dirac en x=1/2, sur l'espace
de fonctions réelles définies sur ]0;1[ , muni de la convergence simple
avec de la topologie faible. est-ce quadratique (=carré de forme linéaire) sur un espace non métrisable ?


3ème idée
ou alors en utilisant une topologie faible sur un dual ?
à ce moment-là, les "points" de l'espace seront des formes linéaires.
et on dispose d'une topologie non métrisable.
Les espaces duaux sont des espaces vectoriels. ça doit être "plat"
comme les espaces euclidiens ??
Déja , on peut envisager des applications affines sur des formes linéaires



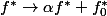
suite

Après, il faut avoir un espace tangent (un fibré?) et une connexion affine.
L'espace tangent se contruit par recollement, dans les cartes, des différentielles de changement de cartes. Si les changements de cartes sont anti-holomorphes, pas de Riemann mais une structure différentiable réelle.

[Aristarque]

Quel bouillonnement d'idées! On avance peut être vers une solution
mais j'ai pour l'instant encore quelques problèmes avec ces différentes idées.

1ère idée
En effet, une surface de Riemann est définie par des cartes holomorphes. Mais ma question concernait les "espaces de Riemann" et non pas les "surface de Riemann". Malheureusement la terminologie est un peu mal faite ici. Une surface de Riemann (à cause du caractère holomorphe des cartes précisément) n'est qu'un cas très particulier d'espace de Riemann à 2 dimension. Pour être sur de bien nous comprendre, je ne tient pas à ce que les coordonnées de ma variété soient holomorphes. Tout ce qu'il faut demander pour pouvoir y définir une métrique dessus c'est que ce soit une variété différentiable réelle de caractère au moins C1.

2ème idée
L'idée du "topologique non métrisable" est intéressante. Mais c'est une question plus facile que celle que je pose. Car ce que je recherche c'est de "l'affine non métrisable" (cf la formulation initiale du problème). En plus, il me semble que le sens que l'on donne à métrisable quand on parle des espaces topologiques non métrisables c'est au sens de "qui puisse être pourvu d'une application distance (application symétrique définie positive et vérifiant l'inégalité triangulaire). Quand on parle de "métrique" en parlant des espaces de Riemann, cela renvoie à l'existence d'une forme quadratique. Là encore, le vocabulaire est ambigue. On devrait contre l'usage parler plutôt de "préhilbertiabilité" que de "métrisabilité".

Bien sûr un espace non métrisable au sens usuel est à fortiori "non préhilbertiable". Mais il est peut etre dangeureux (trop gourmand...) de demander quelque chose d'encore plus fort que ce que je demandais initialement en cherchant un espace à connexion affine qui n'admettrait pas une notion générale de distance (distincte du cas quadratique des espaces de Riemann)

3ème idée
Dans cette idée, il y a le caractère "affine" de l'espace dual qui est intéressant. On se rapproche peut être du but... Je ne vois pas pour l'instant.


Mes éclaircissements terminologiques aident-ils à mieux cerner le problème?

[mathelot]

oui.

1) et dans l'ensemble des fonctions continues périodiques ? Au niveau des séries de Fourier, dès que l'on sort des hypothèses habituelles (C1 par morceaux), il y a des problèmes de convergence.
L'intéret , c'est que les formes quadratiques y sont naturelles (norme L2)
mais pas les convergences des séries,ce qui pourrait rendre la connexion
difficile (?)

avec un argument de topologie
style G-delta denses , théorème de Baire ?? peut être ça permettrait
d'obtenir l'existence d'un contre-exemple.

[Aristarque]

Il me semble que j'ai une réponse à ma question.
La connexion de Levi-Civita (c'est à dire la forme particulière que prend la connexion affine dès qu'elle est "métrisable" au sens où je l'ai défini dans la question initiale) est telle que le tenseur de courbure "Rabcd" défini à partir d'elle vérifie les symétries:

Rabcd+Racdb+Radbc=0
Rabcd-Rbacd=0

Il semble donc que pour trouver un exemple d'espace à connexion affine non métrisable, il suffise de trouver un espace à connexion affine qui viole une de ces deux symétries.

Cela doit exister non?

[mathelot]

Bonsoir,

ça dépend si ce sont des identités ou non. Un façon de trouver un contre-exemple est de lire leur démonstration en détail.

Sinon, pourrais-tu me montrer sur un exemple simple (la sphère S2 par ex)
quels calculs génère une connexion ?