Congruences
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
abicah
- Membre Naturel
- Messages: 68
- Enregistré le: 16 Mar 2017, 13:55
-
 par abicah » 04 Nov 2021, 12:13
par abicah » 04 Nov 2021, 12:13
Bonjour,
Je ne comprends pas la solution d'un exercice trouvé dans un livre de 1 ère année. Voici l'exercice:
Montrer que , pour tout n de N-{0,1},
 Ci -dessous la solution :
Ci -dessous la solution :Remarquer que si
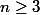
:
}) (1)
(1)et chacun des facteurs

(k appartient à N) est pair, mais congru à 2 modulo 4
Ce que je ne comprends pas :-l'origine de l'égalité
(1) -comment on arrive à conclure à partir de ces éléments de réponse
Merci d'avance pour votre aide
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 04 Nov 2021, 16:41
par tournesol » 04 Nov 2021, 16:41
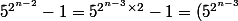^2-1^2)
(type
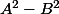
)
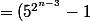(5^{2^{n-3}}+1)=(5^{2^{n-4}\times 2}-1)(5^{2^{n-3}}+1)=((5^{2^{n-4}})^2-1^2)(5^{2^{n-3}}+1))
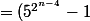(5^{2^{n-4}}+1)(5^{2^{n-3}}+1)=(5^{2^0}-1)(5^{2^0}+1)....(5^{2^{n-4}}-1)(5^{2^{n-4}}+1)(5^{2^{n-3}}+1))
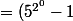[(5^{2^0}+1)....(5^{2^{n-4}}-1)(5^{2^{n-4}}+1)(5^{2^{n-3}}+1)])
Voila donc l'origine de l'égalité 1 .
Chacun des n-2 facteurs est pair:
Avec les congruences , c'est immédiat .
Sinon tout produit d'impairs est impair , en particulier toute puissance de 5 est impaire .
+1 ça fait un nombre pair .
-
abicah
- Membre Naturel
- Messages: 68
- Enregistré le: 16 Mar 2017, 13:55
-
 par abicah » 04 Nov 2021, 16:58
par abicah » 04 Nov 2021, 16:58
Super , merci ta réponse Professeur.
Par contre je viens d'y penser , pourquoi a ton besoin de savoir que les facteurs suivants

sont congru à 2 modulo 4 ?
Merci encore
Modifié en dernier par
abicah le 04 Nov 2021, 17:41, modifié 1 fois.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 04 Nov 2021, 17:41
par tournesol » 04 Nov 2021, 17:41
Pour la question posée , à rien .
Par contre la congruence à 2 modulo 4 montre que chaque facteur est divisible par 2 mais pas par 2^2 .
Ce qui veut dire que l'exposant de 2 dans la décomposition en facteurs premiers de chaque facteurs est égal à 1 .
L'exposant de 2 dans la décomposition de

est donc exactement n ( n-2 +2(à cause du 4)).
ça aurait été utile si la question avait été :
Montrer que pour tout n supérieur ou égal à 2 ,

mais
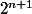
ne le divise pas .
-
abicah
- Membre Naturel
- Messages: 68
- Enregistré le: 16 Mar 2017, 13:55
-
 par abicah » 04 Nov 2021, 18:00
par abicah » 04 Nov 2021, 18:00
Parfait!
-
Maxymyze
- Membre Naturel
- Messages: 52
- Enregistré le: 04 Nov 2021, 21:33
-
 par Maxymyze » 04 Nov 2021, 23:53
par Maxymyze » 04 Nov 2021, 23:53
Soit n un entier naturel supérieur ou égal à 2.
Soit n' le produit de tous les entiers naturels impairs inférieurs à 2^n.
Le nombre de ces entiers impairs est 2^(n-1).
Dans l'anneau des entiers modulo 2^n, ces impairs représentent l'ensemble des classes inversibles.
Ils y forment donc un groupe multiplicatif d'ordre 2^(n-1).
Les translations multiplicatives, comme dans tout groupe, sont des bijections. Donc l'ensemble des inversibles est égal à l'ensemble des inversibles chacun multiplié par 5.
Donc :
n' = {5^(2^[n-1])}n' [modulo 2^n]
soit c l'inverse de 5.
Le produit 5c = 1 est neutre.
Donc le produit n' (modulo 2^n) demeure inchangé si l'on y omet c. Il n'y a plus que 2^(n-2) facteurs dans le produit.
On a donc
n' = {5^(2^[n-2])}n' [modulo 2^n]
soit, en simplifiant par n' qui est impair, donc premier avec 2^n, donc simplifiable :
5^(2^[n-2]) = 1 [modulo 2^n]
Autrement dit
2^n divise 5^(2^[n-2]) - 1

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Nov 2021, 19:36
par Ben314 » 05 Nov 2021, 19:36
Salut,
Maxymyze a écrit: . . .
Donc le produit n' (modulo 2^n) demeure inchangé si l'on y omet c. Il n'y a plus que 2^(n-2) facteurs dans le produit.
On a donc n' = {5^(2^[n-2])}n' [modulo 2^n]
. . .
J'ai beau l'avoir relu 3 fois, ben je comprend rien à ce passage là . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
tulipe
- Membre Naturel
- Messages: 56
- Enregistré le: 06 Juin 2021, 16:07
-
 par tulipe » 05 Nov 2021, 20:52
par tulipe » 05 Nov 2021, 20:52
Tous les nombres sont multipliés par 5, donc à un moment donné 5 sera multiplié par son inverse, ce qui donnera 1. Donc si tu prends tous les nombres en omettant c, et que tu les multiplie pas 5 ça donnera le même résultat.
En clair : produit des 5x (ou x parcours l'ensemble des inversibles) = produit des 5x (ou x parcours l'ensemble des inversibles privé de c)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Nov 2021, 08:23
par Ben314 » 06 Nov 2021, 08:23
1) Si tu enlève 5 et c de l'ensembles des 2^(n-1) nombres dont on fait le produit, il en reste 2^(n-1)-2 qui n'est absolument pas égal au 2^(n-2) de la phrase en rouge.
2) Si tu enlève 5 et c, de ce même ensemble, la fonction "multiplié par 5 modulo 2^n" n'est plus une bijection du nouvel ensemble dans lui même donc la relation n' = {5^(nouveau nombre d'éléments)}n' [modulo 2^n] n'est pas valable.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
tulipe
- Membre Naturel
- Messages: 56
- Enregistré le: 06 Juin 2021, 16:07
-
 par tulipe » 06 Nov 2021, 16:21
par tulipe » 06 Nov 2021, 16:21
De ce que j'ai compris on enlève pas 5 et c, mais juste c, du coup ça fait 2^(n-1) - 1 facteurs, ce qui ne correspond effectivement pas à 2^(n-2). Par contre en enlevant seulement c, on supprime seulement 5c dans le produit des quintuples c'est à dire 1, ça ne change pas le produit des quintuples.
Modifié en dernier par
tulipe le 06 Nov 2021, 16:39, modifié 1 fois.
-
tulipe
- Membre Naturel
- Messages: 56
- Enregistré le: 06 Juin 2021, 16:07
-
 par tulipe » 06 Nov 2021, 16:30
par tulipe » 06 Nov 2021, 16:30
A la réflexion, à chaque multiple impair de c cela supprime un facteur 5.
(Dans le produit des quintuples on va trouver 5c qui est égal à 1, cela supprime un facteur 5.
On y trouvera aussi peut-être 5*3c=3, cela supprime un autre facteur 5)
Donc cela augmente potentiellement le nombre de facteurs 5 qui disparaissent, mais bon ça ne résout toujours pas la question, car de toute façon si on supprime des facteurs 5 d'un côté on supprime également des facteurs de n' donc la puissance de 5 peut diminuer mais cette puissance n'est alors plus multipliée par n'.
-
Maxymyze
- Membre Naturel
- Messages: 52
- Enregistré le: 04 Nov 2021, 21:33
-
 par Maxymyze » 06 Nov 2021, 18:49
par Maxymyze » 06 Nov 2021, 18:49
Vous avez raison.
Il y a problème dans ma "démonstration"
Je n'ai pas le loisir d'étudier s'il est remédiable.
Je vous ai fait perdre votre temps.
Cela m'apprendra à ne pas trop me fier à l'intuition .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
