Congruences

[Mario2015]

Salut,

J`ai une equation a resoudre :

x(x+a)+y=0 mod n

J`ignore la factorisation de n.

Le nombre de solutions est infini.

J`ai cependant une contrainte liant x et y qui pourrait reduire le champ des solutions :

x-y+b=z(z+1)

a,b,n sont connues
x,y,z sont les inconnues.
Les valeurs sont toutes entieres > 1

Peut-on solutionner ce probleme de maniere generale? si oui comment?

Merci pour tout commentaire.
Je cherche le principe de solution pas la solution elle-meme.
Ce n`est pas un devoir.
C`est dans le cadre d`une recherche personnelle.

Merci

[BiancoAngelo]

Salut,

J`ai une equation a resoudre :

x(x+a)+y=0 mod n

J`ignore la factorisation de n.

Le nombre de solutions est infini.

J`ai cependant une contrainte liant x et y qui pourrait reduire le champ des solutions :

x-y+b=z(z+1)

a,b,n sont connues
x,y,z sont les inconnues.
Les valeurs sont toutes entieres > 1

Peut-on solutionner ce probleme de maniere generale? si oui comment?

Merci pour tout commentaire.
Je cherche le principe de solution pas la solution elle-meme.
Ce n`est pas un devoir.
C`est dans le cadre d`une recherche personnelle.

Merci

Salut, tu parles de solutionner le problème. Mais quel problème te poses-tu ?

Avoir la forme des x, la forme des y ?
Celle des z aussi, du coup ? (sachant que je suis pas sûr que rajouter cette contrainte nous aide beaucoup vu que ça rajoute une inconnue, et pas de façon simple, a priori).

Savoir si selon les valeurs de y, il y a toujours des solutions en x...? Vice versa...

S'il y a des n qui créent des solutions simples et évidentes, et d'autres qui sont problématiques...

Il faut savoir ce que tu veux, pour qu'on puisse savoir par quoi commencer

[Mario2015]

Je n`ai pas dit que je ne cherchais pas la solution.
Je me suis mal exprime.
Je cherche plutot l`approche.
Comment resoudre ce probleme?
De quoi a-t-on besoin pour le resoudre?
Pour etre plus concret je peux donner n=5133257
a et b parametres par exemple
a=4530
b=-767

[nodjim]

ça n'a pa l'air simple...
On peut éliminer y et poser
x(x+a+1)+b=z(z+1) mod n
Après, on peut définir pour chaque terme de l'égalité les valeurs mod n, et ensuite comparer. Mais il faut connaitre a et b.

[Mario2015]

ça n'a pa l'air simple...
On peut éliminer y et poser
x(x+a+1)+b=z(z+1) mod n
Après, on peut définir pour chaque terme de l'égalité les valeurs mod n, et ensuite comparer. Mais il faut connaitre a et b.

Merci.
On aurait donc 2 inconnues x et z.
y pourrait prendre n`importe quelle valeur puisqu`elimine.
Donc avec cela a ton avis on pourrait trouver x et z?
Connaissant a et b bien sur.
La factorisation de n nous est inconnue, c`est la base meme du probleme ne l`oublions pas.

[nodjim]

Pour connaitre les valeurs modulo n de x(x+a+1) et z(z+1), je ne vois pas trop comment faire autrement que de les calculer 1 par 1. Il y aura une infinité de solutions en général (faudrait regarder pour les faibles valeurs de n, et encore..) vu qu'on travaille en modulo.

[zygomatique]

Salut,

J`ai une equation a resoudre :

x(x+a)+y=0 mod n

J`ignore la factorisation de n.

Le nombre de solutions est infini.

J`ai cependant une contrainte liant x et y qui pourrait reduire le champ des solutions :

x-y+b=z(z+1)

a,b,n sont connues
x,y,z sont les inconnues.
Les valeurs sont toutes entieres > 1

Peut-on solutionner ce probleme de maniere generale? si oui comment?

Merci pour tout commentaire.
Je cherche le principe de solution pas la solution elle-meme.
Ce n`est pas un devoir.
C`est dans le cadre d`une recherche personnelle.

Merci

salut

bien sur qu'on sait résoudre théoriquement ce problème ... puisqu'on sait résoudre une équation du second degré ...

maintenant les valeurs particulières des différents paramètres peuvent corser (ou non) le pb ....

[paquito]

pour toutes valeur de x, a et de y on trouve une valeur de n solution! Il suffit de prendre n=k((x+a)+y).

Tu as trois inconnues pour une équation; faut pas réver !

[Mario2015]

pour toutes valeur de x, a et de y on trouve une valeur de n solution! Il suffit de prendre n=k((x+a)+y).

Tu as trois inconnues pour une équation; faut pas réver !

Mais tu supposes connue la factorisation de n.
D`ou vient le k?

[zygomatique]

pour toutes valeurs de a et n on sait résoudre l'équation x(x + a) + y = 0 [n]

on sait exprimer x en fonction de y ...

bien la primalité de n ou non conduit évidemment à des solutions ou non ...

[paquito]

Mais tu supposes connue la factorisation de n.
D`ou vient le k?

n=k(x+a)+y est toujours possible! Il n'y a aucune condition sur n!!!

[Mario2015]

pour toutes valeur de x, a et de y on trouve une valeur de n solution! Il suffit de prendre n=k((x+a)+y).

Tu as trois inconnues pour une équation; faut pas réver !

Relisez! c`est bien un produit n=k((x+a)+y) et non ce que vous dites

[Mario2015]

pour toutes valeurs de a et n on sait résoudre l'équation x(x + a) + y = 0 [n]

on sait exprimer x en fonction de y ...

bien la primalité de n ou non conduit évidemment à des solutions ou non ...

Ce n`est pas ce qu`il a ecrit bon sang?

[zygomatique]

n=k(x+a)+y est toujours possible! Il n'y a aucune condition sur n!!!

je ne comprends pas ...

on veut résoudre l'équation d'inconnues x et y :: x(x + a) + y = 0 [n]

a et n étant donnés !!

[Mario2015]

n=k(x+a)+y est toujours possible! Il n'y a aucune condition sur n!!!

D`ou sors-tu ce k???????

[Mario2015]

pour toutes valeurs de a et n on sait résoudre l'équation x(x + a) + y = 0 [n]

on sait exprimer x en fonction de y ...

bien la primalité de n ou non conduit évidemment à des solutions ou non ...

n=258
a=32

J`attends ta solution non pas le resultat (un ordi le fait en un clin d`oeil).

Merci.

[paquito]

J'ai mal exprimé ce que je voulais dire;
tu choisis n'importe quelle valeur pour x, et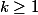 tel que kn>x(x+a), ce qui est toujours possible; dans ce cas y=kn-x(x+a) est solution de x(x+a)+y=0[n];
exemple: x=10, a=32 et n=258; on a x(x+a)+96=2*258 ou si x=25, x(x+a)+123=6*258; donc cette équation a peu d'intérêt!
Si on rajoute la contrainte x-y+b=z(z+1), ça devient plus intéressant, mais là encore, elle peut s'écrire y=x+b-z(z+1), donc on peut choisir z arbitrairement, on aura une infinité de possibilité pour x (x>b-z(z+1)) qui fourniront des solutions pour cette équation et on obtient la condition:
kn-(x+a+1)-b+z(z+1)=0 où en fait, il y a 3 inconnues, donc blocage!

Si on veut des solutions, il faut tricher; par exemple pour n=258, x=10, y=96 sont solutions donc prenons z=4; x-y+b=z(z+1) b=106. je n'ai évidemment rien prouvé, sauf que ton problème avait une infinité de solutions; de toutes façons une équation, une autre en terme de congruence avec 3 inconnues et 3 paramètres sans compter k, il ne faut pas espérer une méthode de résolution, il n'y en a pas!

[Mario2015]

Le probleme est, en fait, un peu plus complexe.
Pour l`instant, j`abandonne.
J`ai trouve un moyen de reformuler tout cela.
Si on peut solutionner de maniere generale :
ax^2+bx+c = 0 mod n sans connaitre la factorisation de n
oui, il y a espoir de solution.
On ne peut pas pour l`instant.
Merci pour les contributions.

[paquito]

Tes 2 relations ne sont pas linéaires, ce qui effectivement complique les choses! Bon courage quand même.

[chan79]

Le probleme est, en fait, un peu plus complexe.
Pour l`instant, j`abandonne.
J`ai trouve un moyen de reformuler tout cela.
Si on peut solutionner de maniere generale :
ax^2+bx+c = 0 mod n sans connaitre la factorisation de n
oui, il y a espoir de solution.
On ne peut pas pour l`instant.
Merci pour les contributions.

Dans le cas où n est premier, ça se fait sans trop de mal (sur un exemple ...)
x²+3x+9=0 (7)
x²+10x+9=0 (7)
(x+5)²-16=0 (7)
(x+5-4)(x+5+4)=0 (7)
(x+1)(x+9)=0 (7)
comme p est premier
x=-1 (7) x=-9 (7)

soit S={6;5} modulo 7

autre exemple
x²+x=0 (15)
x²+16x=0 (15)
(x+8)²=64 (15)
(x+8)²=4 (15)
On cherche les carrés des entiers modulo 15
0²=0 ; 1²=1 ; 2²=4 ; 3²=9 ; 4²=16 ; 5²=10 ; 6²=6
7²=4; 8²=4 ; 9²=6 ; 10²=10 ; 11²=1 ; 12²=9 ; 13²=4 ; 14²=1

on a donc x+8=2 (15) ou x+8=7 (15) ou x+8=8 (15) ou x+8=13 (15)

S={9;14;0;5} modulo 15