Congruences
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maths699
- Membre Naturel
- Messages: 41
- Enregistré le: 21 Oct 2013, 18:29
-
 par maths699 » 03 Nov 2013, 11:20
par maths699 » 03 Nov 2013, 11:20
Bonjour , Pourriez vous m'aidez svp?
Soit p un nombre premier et a,b des entiers
1)Montrer que le coefficient binomial "p parmi i" est divisible par p pour tout entier i avec 0
2)Montrer que (a+b)^p congru à a^p +b^p (mod p)
3)Montrer par recurrence sur n que n^9-n est divisible par p pour tout entier n
4)Supposons de plus que n n'est pas multiple de p. Montrer que n^(p-1) congr 1(mod 8)
je n'arrive pas pour la 2) et la 4)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 03 Nov 2013, 11:59
par fatal_error » 03 Nov 2013, 11:59
slt,
pour 1) ca serait pas plutot:
"i parmi p" est divisible par p pour tout entier i avec 0<i<p
du coup pour la 2) t'écris le binome de newton et ya plein de termes qui sont divisibles par p.
la vie est une fête


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 03 Nov 2013, 12:12
par fatal_error » 03 Nov 2013, 12:12
quant à 4) il semblerait que ton énoncé soit encore faux...
si on prend n=2, p=5, p premier
n^(p-1)=2^4=16
or 16 est divisible par 8...
la vie est une fête

-
maths699
- Membre Naturel
- Messages: 41
- Enregistré le: 21 Oct 2013, 18:29
-
 par maths699 » 03 Nov 2013, 12:22
par maths699 » 03 Nov 2013, 12:22
euh ou désolé c'est n^(p-1) congr 1(mod p)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 03 Nov 2013, 13:05
par fatal_error » 03 Nov 2013, 13:05
une dem un peu byzarre...
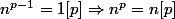
Pour démontrer le dernier résultat, on peux utiliser la propriété
^{p}=a^{p}+b^{p}[p])
démontrée en 2).
genre
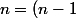+1\\<br />n^{p}=(n-1+1)^{p}=(n-1)^{p}+1[p])
de même avec
^{p}=(n-2+1)^{p}=(n-2)^{p}+1[p])
idem on peux ecrire
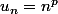
et on peut noter que u_n respecte la relation de récurrence suivante
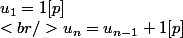
et on obtient
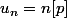
Du coup il reste à démontrer que si n non multiple de p on a
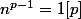
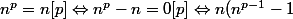=0[p])
n non multiple de p implqiue
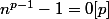
edit coquille. 0^p = 0...non 1

la vie est une fête

-
maths699
- Membre Naturel
- Messages: 41
- Enregistré le: 21 Oct 2013, 18:29
-
 par maths699 » 03 Nov 2013, 14:42
par maths699 » 03 Nov 2013, 14:42
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
