Congruence Modulaire

[MathsetZinc]

Bonjour à tous,

J'ai cet exercice à faire, or je bloque sur les deux dernières questions

Voici l'énoncé: https://zupimages.net/viewer.php?id=22/40/jddd.png

Voici ce que j'ai fait jusqu'à maintenant:

1) 2021299320121= 2083813732*97+81
K=97-81=16

2)a) 10^12=1030927835*97+50
10^12 (congru) 50 (modulo 97)

10^6=10309*97+27
10^6 (congru) 27 (97)

1 congru à 1 (97)

A (congru) S*10^12+N*10^6+M (97)
donc A (congru) 50*S+27*N+M [97]

b) A congru à 50*S+27*N+M (97)

et r congru à 50*S+27*N+M (97) (car r: reste de la div. euclidienne de A par 97)
soit r1 congru à 50*S+27*N+M (97)

donc: r congru r1 (97)

r<97 donc r=0*97+r1 soit r=r1

Ainsi K=97-r soit K=97-r1

3a) Soit A=10^12S=10^6N=M
A'=10^12S'=10^6N=M

A-A'=10^12S-10^12S'
=10^12(S-S') où S-S' différent de 0

S ne peut valoir que 1 ou 2
Donc S-S' ne peut valoir que 1 ou -1

A n'est donc pas congru à A' modulo 97

Ils n'ont donc pas le même reste alors c'est détecté

b) Or, à partir de ce moment-ci, je n'ai pas d'idée, hormis expliquer en français sur la feuille que
- si S change, alors A changera, donc plus le même reste et donc erreur détectée
- Pareil pour N
- Pareil pour M

Enfin, pour la dernière, aucune idée!

S'il est possible de m'aider... Merci!

[MathsetZinc]

Re!

Toujours besoin d'aide! Si quelqu'un peut m'aider

[lyceen95]

Question 1 : ok
Question 2 : je n'aime pas trop la rédaction, mais ok.
Question 3a : même remarque que pour la question 2)
En particulier, si on se trompe en tapant 5 par exemple, tu ne dis pas que la clé de contrôle va le détecter, vu que tu supposes que quand on se trompe, on se trompe forcément en remplaçant 1 par 2 ou l'inverse.

Question 3b
Si on a un numéro de départ N.
Si on se trompe sur un seul chiffre, cela revient à additionner ou retrancher un nombre de la forme avec k entre 1 et 9
Or, aucun nombre de cette forme n'est multiple de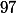 ( la décomposition d'un nombre de cette forme en facteurs premier va donner si k vaut 1, 3, 7ou 9, ou quelque chose similaire pour les autres valeurs de k ; le facteur 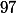n'apparaît pas dans cette décomposition en facteurs premiers)
Donc la clé de contrôle devient forcément fausse si on se trompe sur un seul chiffre.

Question 3c
Si on intervertit les 2 premiers chiffres, cela revient à ajouter ou retrancher à notre numéro, avec k entre 1 et 9.
Et comme n'est pas un multiple de 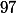, l'argument précédent s'applique toujours.

[MathsetZinc]

Bonjour Lycéen95!

Merci de ta réponse.

Faut-il démonter pour ces questions ou l'explication que tu as mise est suffisante?

Car de mon côté, pour la 3b, j'ai essayé quelque chose de farfelu:

Décomposons N en ses différents nombres : n0, n1, n2, n3, n4, n5 :












( tous modulo 97)

On a donc

Supposons que l'erreur intervienne sur n2:



donc:

et: [/tex]

En soustrayant et en factorisant, on a:



Supposons que n2 et n2' peuvent prendre les valeurs 1,2,3,4,5,6,7,8,9

Ainsi n2-n2' peut prendre -9,-8,-7,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6,7,8,9

Ainsi, A-A' (pas congru) 0 [97]

L'erreur sera donc détectée!

Pour la 3c, faut il donc effectuer une telle démonstration également?

Merci encore

[lyceen95]

Mon explication est peut-être un peu courte, mais elle est suffisante. Et en tout cas, la tienne est trop détaillée.
Si tu as fait tous ces calculs, c'est que tu n'as pas vu l'argument essentiel.

L'esprit du truc, c'est que 97 est un nombre premier, et évidemment, plus grand que 10.
Donc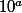 , peut importe la valeur de , ce ne sera jamais un multiple de 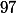, et même mieux, 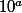sera toujours premier avec 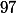, même si on devait travailler avec des nombres de 20 ou 30 chiffres.

Là, tu as fait beaucoup d'efforts , pour un résultat limité : le truc marche pour tous les nombres jusqu'à 13 chiffres.
Avec moins d'efforts, on traite tous les nombres, même ceux beaucoup plus grands.

Quand on passe de A à A', en changeant un seul chiffre, on ajoute un truc qui ne peut pas être un multiple de 97 ( il faut que tu en sois convaincu, sinon tu ne peux pas convaincre ton lecteur!), et donc la clé de contrôle ne peut pas être la même pour A et pour A'. (et cette partie là aussi, il faut que tu en sois convaincu, sinon, tu ne peux pas convaincre ton lecteur).

[MathsetZinc]

D'accord, merci beaucoup pour ton aide!

Par ailleurs:

Question 3a : même remarque que pour la question 2)
En particulier, si on se trompe en tapant 5 par exemple, tu ne dis pas que la clé de contrôle va le détecter, vu que tu supposes que quand on se trompe, on se trompe forcément en remplaçant 1 par 2 ou l'inverse. .

On ne peut pas taper 5, puisque le premier chiffre ne peut être que 1 (pour les hommes) ou 2 (pour les femmes)