Conditions solutions périodiques pour équation différentielles

[Anicée]

Bonjour,

j'ai une question théorique que je n'arrive pas à trouver sur internet et ni à trouver par moi même et j'aimerai la comprendre pour avancer dans mes exercices
,
a quelles conditions sur les nombres a,b,c appartenant à R l'équation différentielle admet-elle exclusivement des solutions périodiques?
ay''+by'+cy = 0

j'avais pensé au sinus et cosinus mais j'ai l'impression d'être dans la mauvaise direction...

[Heure]

Tu dois avoir dans tes cours la résolution des EDLH2
Regarde dans le cas général quelles sont les solutions périodiques...

[Anicée]

justement j'ai pas de cours théorique et la bibliothéque est fermée pdt les vacances ... donc point de vue théorie je n'ai que internet :s

[Nightmare]

Eh bien, fais une recherche sur internet alors :lol3:

[Ben314]

Bon, je suis brave...
Les solutions (complexes) de l'équa diff. ay''+by'+cy = 0 forment un espace vectoriel de dimension deux engendré par :
a) Les fonctions et lorsque le polynôme 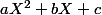admet deux racines (complexe) distinctes et .
b) Les fonctions et lorsque le polynôme 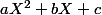admet une seule racines (complexe) double .

[Black Jack]

Si c'est vraiment des solutions périodiques (et donc sans amortissement) qui sont demandées.
A ne pas confondre avec des solutions amenant une réponse d'oscillations amorties qui ne sont pas périodiques.

... alors les solutions de l'équation caractéristique doivent être imaginaires pures.

Donc IL FAUT b = 0 ET "a" et"c" doivent être de même signe.

:zen: