Je comprends pas !!! :( programmation linéaire

[rom2606]

Résoudre le problème suivant : min f( x1;x2 ) = -x1 + 3x2 avec :
0 < x1
0 < x2
-x1 + x2 < 1
x1 + x2 < 2
voila on la pas vue en cour et je sais pas comment faire . :triste:

[rom2606]

personne y arrive ? :triste:

[BQss]

Salut,
Ta fonction est linéaire et on est sur un compact(une fonction continue sur un compact est borné et atteint ses bornes).
Il existe donc un minimum et il se trouve sur la frontiere de ton compact(car sur un ouvert un minimum doit obligatoirement voir la differentielle s'annuler en ce point, or la differentielle est constante et non nulle, ce maximum est donc atteint sur la fermeture) . Ici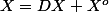 . Avec DX la fermeture et le plus grand ouvert contenu dans X sur lequel il n'y a donc aucun minimum...

Tu n'as plus qu'a parametrer sur les 4 segments qui composent cette frontiere a l'aide des droites y=2+x,y=2-x,y=0,x=0 (je te conseille de faire un dessin pour taider), et tu prends la valeur minimum de ces 4 problemes a une variable(ou tu auras cherché le minimum locale).

[BQss]

Je t'aide un peu...

Tu vas tomber sur ces 4 equations:
-x1 0-4x1+6 1/22x1+3 03x2 0

Le minimum vaut pour chacune:
(1) -2 en (2,0)
(2) -2 en (2,0)
(3) 3 en (0,1)
(4) 0 en (0,0)


Finalement le minimum est atteint en (2,0) et vaut -2...

[rom2606]

okj merci je vais essayer de le refaire tout seul :++:

[rom2606]

je comprends pas comment tu fais pour trouver tes droites y=2+x et y=2-x ?

[BQss]

je comprends pas comment tu fais pour trouver tes droites y=2+x et y=2-x ?

Euh non excuse moi c'est "y=1+x "(mon resultat utilise bien 1+x et pas 2+x, ca vient de -x1+x2 < 1, pour obtenir l'equation (3) j'ai remplace x2 par 1+x1...) et y=2-x que j'ai utilisé. J'ai utilisé les bornes du domaine de definition en posant y=x2 et x=x1.

Fais un graphique tu verras ...

[rom2606]

et je comprend pas nn plus comment tu trouve tes 4 équationss ? :triste:

[BQss]

-Le minimum est sur la frontiere du domaine.
-Cette frontiere est composé de 4 segments (as tu fais un dessin?)

J'ai donc d'abord( a partir des bornes que tu as definies établi les equations de ces 4 segments ainsi que leur domaine de definition):

exemple:

-x1+x2<1(precision c'est des inferieurs ou egal qu'il faut ecrire pour que le probleme admette une solution, une fonction lineaire n'a pas de minimum sur un ouvert...)
on cherche donc le minimum sur la droite x2=1+x1, mais ou x1 doit remplir certaines conditions: "a gauche" 0 x1<2-1-x1
et donc x1<1/2 qui correspond au condition que doit remplir x1 dans l'equation (3) (encore une fois fais un dessin..., 1/2 n'est rien d'autre que l'abscisse du point d'intersection de x2=1+x1 avec la droite x2=2-x1, qui delimite a droite ce segment ...).


J'ai donc ici un des quatres segments: x2=1+x1 avec 0C'est la dessus que je vais chercher mon minimum(et sur les trois autres), je remplace x2 par 1+x1 dans la fonction ce qui donne:
f(x1,x2)=f(x1,1+x1)=g(x1)= 2x1+3 avec la condition 0Et je recherche le minimum qui vaut 3 pour x1=0 et est donc atteint en (0;1+x1)=(0;1).
Ceci correspond a l'equation (3).

On fait exactement pareille sur les trois autres segments et on prend le minimum des quatres minimums.

Finalement le minimum est atteint en (2,0) et vaut -2... Il est obtenue pour les equations (1) et (2) (et correspond donc en fait a la valeur obtenue au point d'intersection des droites d'equations x2=2-x1 et x2=0), il vaut f(2,0)=-2.

[rom2606]

ok merci j'ai compris mais j'ai jamais étudié sa en cour donc c'est un peu chaud pour moi. Si sa te dérange pas voila un autre exo ou j'ai du mal ( j'en avait 12 à faire seul 2 mon posé problème :we: lol )

3 substances X,Y et Z contiennent 4 ingrédients A, B, C, D. Le % de chaque ingrédient et le cout, en centimes par gramme, de chaque substance sont indiqués ds le tableau ci dessous:
A B C D cout
X 20% 10% 25% 45% 25 ct
Y 20% 40% 15% 25% 35ct
z 10% 20% 25% 45% 50ctSi le cout doit etre minimal, combien de grammes de chaque substance audrait-il amalgamer pr obtenir un mélange de 20gr contenant o - 14% de A, 16% de B, 20% de C ? quel serait le mélange le plus couteux ?

[rom2606]

c'est un pb d'optimisation linéaire, mais je trouve trois variable et je sais pas comment représenté sa graphiquement :triste: vous nn plus ?

[rom2606]

Mon prof qui nous a donné cet exo sans vraiment le regarder nous dit qu'il n'y a aucune solution mais j'en suis pas très sur , vous en pensez quoi ? :hum:

[rom2606]

3 substances X,Y et Z contiennent 4 ingrédients A, B, C, D. Le % de chaque ingrédient et le cout, en centimes par gramme, de chaque substance sont indiqués ds le tableau ci dessous:
A B C D cout
X 20% 10% 25% 45% 25 ct
Y 20% 40% 15% 25% 35ct
z 10% 20% 25% 45% 50ctSi le cout doit etre minimal, combien de grammes de chaque substance audrait-il amalgamer pr obtenir un mélange de 20gr contenant o - 14% de A, 16% de B, 20% de C ? quel serait le mélange le plus couteux ?

Est ce faisable ou impossible ?