Comprendre une somme

[snowwind]

Bonjour,

Comme beaucoup d'autres je débute les concours dans moins de 2 semaines et une petite bricole me chagrine. Mon prof a écrit que la somme des 1/k (k e (n+1;2n)) = somme des ((-1)^(k+1))/k (k e (1;2n))

Effectivement ça marche j'ai vérifié pour différentes valeurs de n mais pourquoi ça marche ? C'est ce que j'aimerais que l'on m'explique si possible.

Bonne fin d'après midi et merci par avance.

[Le_chat]

Salut.

En partant de ta seconde expression, que je note S:

Somme des (-1)^k+1/k=1-1/2+1/3-1/4+...+1/(2n-1)-1/2n

En regroupant les termes avec un signe"+" et ceux avec un "-":

S=1+1/3+...+1/(2n-1)-(1/2+...+1/2n)
Dans la parenthèse à droite, on peut tout factoriser par 1/2.
On peut aussi écrire que:
1+1/3+...+1/(2n-1)=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1/2+1/4+1/6+...+1/2n)

En fait on dit que la somme des inverses des nombres impairs, ça fait la somme des inverses de tout le monde moins la somme des inverses des nombres pairs.

Donc en remplaçant dans S, on tombe sur:

S=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1/2+1/4+1/6+...+1/2n)-(1/2+1/4+1/6+...+1/2n)
S=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1+1/2+1/3+...+1/n)

Et il y a bien les n premiers termes qui s'en vont:

S=1/(n+1)+...+1/(2n)

[snowwind]

Salut.

En partant de ta seconde expression, que je note S:

Somme des (-1)^k+1/k=1-1/2+1/3-1/4+...+1/(2n-1)-1/2n

En regroupant les termes avec un signe"+" et ceux avec un "-":

S=1+1/3+...+1/(2n-1)-(1/2+...+1/2n)
Dans la parenthèse à droite, on peut tout factoriser par 1/2.
On peut aussi écrire que:
1+1/3+...+1/(2n-1)=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1/2+1/4+1/6+...+1/2n)

En fait on dit que la somme des inverses des nombres impairs, ça fait la somme des inverses de tout le monde moins la somme des inverses des nombres pairs.

Donc en remplaçant dans S, on tombe sur:

S=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1/2+1/4+1/6+...+1/2n)-(1/2+1/4+1/6+...+1/2n)
S=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1+1/2+1/3+...+1/n)

Et il y a bien les n premiers termes qui s'en vont:

S=1/(n+1)+...+1/(2n)

Effectivement ^^ je n'irai pas jusqu'à dire que c'est évident mais avec l'explication ça passe beaucoup mieux ... Reste maintenant à savoir où il est allé pêché ça et comment, mais ça, c'est un secret de prof de maths je pense ^^ Merci beaucoup en tout cas pour ta réponse ultrarapide ça va me permettre d'avancer

[Cryptocatron-11]

Bonjour,

Je comprends pas la démo de mon cours concernant l'inégalité de Cauchy-Swharz. On a :



Je comprends pas déjà comment il passe de la deuxième à la troisième ligne ... J'aurais plutôt cru que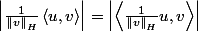 Non ?

Bon continuons ...

Il pose Bon bah ça OK

D'ou

Puis



Et là non plus je comprends pas du tout comment il passe de ces deux dernières inégalités ...

[chan79]

Salut.

En partant de ta seconde expression, que je note S:

Somme des (-1)^k+1/k=1-1/2+1/3-1/4+...+1/(2n-1)-1/2n

En regroupant les termes avec un signe"+" et ceux avec un "-":

S=1+1/3+...+1/(2n-1)-(1/2+...+1/2n)
Dans la parenthèse à droite, on peut tout factoriser par 1/2.
On peut aussi écrire que:
1+1/3+...+1/(2n-1)=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1/2+1/4+1/6+...+1/2n)

En fait on dit que la somme des inverses des nombres impairs, ça fait la somme des inverses de tout le monde moins la somme des inverses des nombres pairs.

Donc en remplaçant dans S, on tombe sur:

S=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1/2+1/4+1/6+...+1/2n)-(1/2+1/4+1/6+...+1/2n)
S=1+1/2+1/3+1/4+...+1/(2n-1)+1/2n-(1+1/2+1/3+...+1/n)

Et il y a bien les n premiers termes qui s'en vont:

S=1/(n+1)+...+1/(2n)

Salut
Même chose en partant de la première expression
1/(n+1)+1/(n+2)+ …+1/(n+n)=
1+1/2+1/3+ … +1/(n+n)-(1+1/2+1/3+… +1/n)
1+1/2+1/3+ … +1/(n+n) -1/2 *(1+1/2+1/3+… +1/n) - 1/2 *(1+1/2+1/3+… +1/n)
1+1/2+1/3 + … +1(n+n) – 1/2-1/4-1/6 - … -1/(2n) – 1/2-1/4-1/6 - … -1/(2n)
1+1/3+1/5+ … + 1/(2n-1) – 1/2-1/4-1/6 - … -1/(2n)
1-1/2+1/3-1/4+1/5 … +1/(2n-1)-1/(2n)