Bah, la récurrence du raisonnement du manuel est une récurrence simple.
On montre par récurrence (simple, j'insiste) sur l'entier

que si
)
sont racines distinctes de

, alors
\cdots(X-a_k))
divise

.
Il y a une initialisation (le thèorème 5) puis une hérédité où on utilise de nouveau le théorème 5.
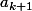
est racine de

parce que ça fait partie des hypothèses. Relis l'énoncé !
On aurait pu aussi raisonner ainsi :
On veut montrer, pour tout entier

, la propriété
)
: "Pour tout polynôme

, si

sont des racines distinctes de

, alors
\cdots(X-a_r))
divise

."
)
est le théorème 5.
Supposons
)
vraie. Soient

des racines distinctes de

. D'après le théorème 5, il existe un polynôme

tel que
Q)
. Pour
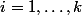
on a
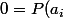=(a_i-a_{k+1})Q(a_i))
d'où
=0)
puisque

. Donc
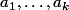
sont des racines distinctes de

et par l'hypothèse de récurrence
\cdot(X-a_k))
divise

. On en déduit que
\cdots(X_a_{k+1}))
divise

, ce qui montre
)
.
On a ainsi montré
)
pour tout entier

.

