La composition de DLs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Celph
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Juil 2006, 15:28
-
 par Celph » 16 Juil 2006, 15:32
par Celph » 16 Juil 2006, 15:32
Bonjour,
J'étudie la convergence de la série de terme général,
u(n)=sin[pi*(1+n²)^1/2],
Je me suis laissé dire que la solution s'obtenait par DL de l'intérieur de sin. Sous quelles conditions puis-je affirmer que u(n) équivaut à sin de l'équivalent de pi*(1+n²)^1/2 ?
Merci de votre aide.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 15:54
par nekros » 16 Juil 2006, 15:54
Salut,
Tu parles d'équivalents, et ensuite de DL ?! :doh:
Thomas G :zen:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 16:06
par nekros » 16 Juil 2006, 16:06
Peut-être une piste :
En l'infini :
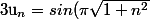=sin(\pi n\sqrt{1+\frac{1}{n^2}})=sin(\pi n (1+\frac{1}{n^2}+o(\frac{1}{n^2})))
Donc
)=(-1)^n sin(\frac{\pi}{2n}+o(\frac{1}{n}))
Juste une idée...
Thomas G :zen:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 16:07
par Sdec25 » 16 Juil 2006, 16:07
Il faut faire attention avec les équivalents sur les suites (quand on compose).

est équivalent à
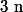
mais
)
n'équivaut pas à
 = 0)
, donc il faut passer par un DL dans ce cas.
-
Celph
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Juil 2006, 15:28
-
 par Celph » 16 Juil 2006, 16:07
par Celph » 16 Juil 2006, 16:07
Bien vu, j'ai effectivement fait une erreur, je ne voulais pas dire 'équivaut à' mais bien "est égal à". :doh:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 16:11
par nekros » 16 Juil 2006, 16:11
Ensuite, pour étudier la convergence, tu peux te servir tu critère spécial des séries alternées.
En effet, tu as
^n sin (w_n))
avec
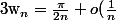)
Tout dépend l'intervalle sur lequel tu étudies la convergence...
Thomas G :zen:
-
Celph
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Juil 2006, 15:28
-
 par Celph » 16 Juil 2006, 16:15
par Celph » 16 Juil 2006, 16:15
Ok Nekros,
Et comme il faut que w(n) soit positive pour appliquer le théorème des séries alternées, il convient de montrer que w(n) est positive à partir d'un certain rang et ainsi on a la réponse, c'est bien cela ?
De quel intervalle parles-tu ?
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 16:21
par nekros » 16 Juil 2006, 16:21
Oui entre autres...
Sinon, pour l'intervalle, oublie...
Bon courage !
Thomas G :zen:
-
Celph
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Juil 2006, 15:28
-
 par Celph » 16 Juil 2006, 16:29
par Celph » 16 Juil 2006, 16:29
Merci. :++:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 16:52
par nekros » 16 Juil 2006, 16:52
De rien :we:
Thomas G :zen:
-
Celph
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Juil 2006, 15:28
-
 par Celph » 16 Juil 2006, 18:16
par Celph » 16 Juil 2006, 18:16
Merci :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
