Composée de deux opérateurs différentiels linéaires
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 04:44
par barbu23 » 24 Fév 2015, 04:44
Bonjour à tous,
J'ai besoin de déduire l'expression de la fonction suivante :
 f)
, sachant que :
 \circ ( \mathrm{id} - j \partial_x ) f = e^x)
, et
 = 1)
.
Je précise que :

.
Merci d'avance. :happy3:
Edit : Excusez moi d'avoir ouvert ce fil sans me rendre compte que la question est facile à résoudre
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 17:44
par barbu23 » 24 Fév 2015, 17:44
Bonjour à tous,
Je cherche une condition nécessaire et suffisante sur
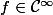
pour qu'on ait l'équivalence suivante :
 f \\ \frac{1}{1 - j^{2}} e^{jx} = ( \mathrm{id} - \partial_x ) f \\ \frac{1}{1 - j^{2}} e^{j^{2}x} = ( \mathrm{id} - j^{2} \partial_x ) f \end{cases} <br />\ \ \Longleftrightarrow \ \<br />\begin{cases} ( \mathrm{id} - j^2 \partial_x ) ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
L'implication suivante est toujours vérifiée :
 f \\ \frac{1}{1 - j^{2}} e^{jx} = ( \mathrm{id} - \partial_x ) f \\ \frac{1}{1 - j^{2}} e^{j^{2}x} = ( \mathrm{id} - j^{2} \partial_x ) f \end{cases} <br />\ \ \Longrightarrow \ \<br />\begin{cases} ( \mathrm{id} - j^2 \partial_x ) ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
Par contre, l'implication inverse :
 f \\ \frac{1}{1 - j^{2}} e^{jx} = ( \mathrm{id} - \partial_x ) f \\ \frac{1}{1 - j^{2}} e^{j^{2}x} = ( \mathrm{id} - j^{2} \partial_x ) f \end{cases} <br />\ \ \Longleftarrow \ \<br />\begin{cases} ( \mathrm{id} - j^2 \partial_x ) ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
je ne sais pas, quant est ce que, elle est valable.
Merci d'avance pour votre aide. :happy3:
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 24 Fév 2015, 18:00
par SLA » 24 Fév 2015, 18:00
barbu23 a écrit:Bonjour à tous,
Je cherche une condition nécessaire et suffisante sur
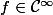
pour qu'on ait l'équivalence suivante :
 f \\ \frac{1}{1 - j^{2}} e^{jx} = ( \mathrm{id} - \partial_x ) f \\ \frac{1}{1 - j^{2}} e^{j^{2}x} = ( \mathrm{id} - j^{2} \partial_x ) f \end{cases} <br />\ \ \Longleftrightarrow \ \<br />\begin{cases} ( \mathrm{id} - j^2 \partial_x ) ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
L'implication suivante est toujours vérifiée :
 f \\ \frac{1}{1 - j^{2}} e^{jx} = ( \mathrm{id} - \partial_x ) f \\ \frac{1}{1 - j^{2}} e^{j^{2}x} = ( \mathrm{id} - j^{2} \partial_x ) f \end{cases} <br />\ \ \Longrightarrow \ \<br />\begin{cases} ( \mathrm{id} - j^2 \partial_x ) ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
Par contre, l'implication inverse :
 f \\ \frac{1}{1 - j^{2}} e^{jx} = ( \mathrm{id} - \partial_x ) f \\ \frac{1}{1 - j^{2}} e^{j^{2}x} = ( \mathrm{id} - j^{2} \partial_x ) f \end{cases} <br />\ \ \Longleftarrow \ \<br />\begin{cases} ( \mathrm{id} - j^2 \partial_x ) ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
je ne sais pas, quant est ce que, elle est valable.
Merci d'avance pour votre aide. :happy3:
Salut,
Tu as montré dans un autre post que tu sais résoudre chacune de ces EDO, tu as juste a faire le boulot.
Cordialement
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 18:11
par barbu23 » 24 Fév 2015, 18:11
Oui, mais, ici, il n'est pas question de résolution de chacune de ces équations, mais simplement de trouver un moyen d'avoir l'équivalence entre ces deux systèmes que j'ai écrit plus haut. Tu peux m'aider là dessus stp ? Merci infiniment. :happy3:
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 24 Fév 2015, 18:28
par SLA » 24 Fév 2015, 18:28
barbu23 a écrit:Oui, mais, ici, il n'est pas question de résolution de chacune de ces équations, mais simplement de trouver un moyen d'avoir l'équivalence entre ces deux systèmes que j'ai écrit plus haut. Tu peux m'aider là dessus stp ? Merci infiniment. :happy3:
Dans ce cas, l'autre implication est clairement fausse. Tu l'as toi même montré dans ton autre fil.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 18:34
par barbu23 » 24 Fév 2015, 18:34
SLA a écrit:Dans ce cas, l'autre implication est clairement fausse. Tu l'as toi même montré dans ton autre fil.
Ohhh ! Je n'ai pas compris. :hum:
Même si on ajoute une condition initiale à

, ça reste fausse l'implication inverse ?
Merci d'avance. :happy3:
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 24 Fév 2015, 19:04
par SLA » 24 Fév 2015, 19:04
barbu23 a écrit:Ohhh ! Je n'ai pas compris. :hum:
Même si on ajoute une condition initiale à

, ça reste fausse l'implication inverse ?
Merci d'avance. :happy3:
Par contre si tu rajoutes des conditions initiales, ça peut devenir vrai.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 19:40
par barbu23 » 24 Fév 2015, 19:40
SLA a écrit:Par contre si tu rajoutes des conditions initiales, ça peut devenir vrai.
Et dans notre cas, quelle est cette condition initiale pour

?
Merci d'avance. :happy3:
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 24 Fév 2015, 19:57
par SLA » 24 Fév 2015, 19:57
barbu23 a écrit:Et dans notre cas, quelle est cette condition initiale pour

?
Merci d'avance. :happy3:
Il ne faut pas abuser. Tu dois être capable de résoudre ça tout seul comme un grand.
Au boulot!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 20:31
par barbu23 » 24 Fév 2015, 20:31
SLA a écrit:Il ne faut pas abuser. Tu dois être capable de résoudre ça tout seul comme un grand.
Au boulot!
Oui, je sais, il faut que je compte sur moi même lorsqu'il s'agit de ce genre de choses, mais ici c'est différent :
Dans :
 ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
On a des opérateurs qu'on ne peut pas inverser :
)
et
)
et
)
parce qu'ils ne sont pas bijectives.
Par exemple, si on cherche à passer de :
 ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f)
à
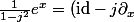 f)
, on a que :
 f \in \mathrm{ker} ( \mathrm{id} - j^2 \partial_x ) = \mathbb{R}. e^{jx})
, et après ?. Bref, je ne sais pas comment poursuivre ce travail seul.
Merci d'avance pour vos éclaircissements.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 22:02
par barbu23 » 24 Fév 2015, 22:02
SLA a écrit:Il ne faut pas abuser. Tu dois être capable de résoudre ça tout seul comme un grand.
Au boulot!
Oui, je sais, il faut que je compte sur moi même lorsqu'il s'agit de ce genre de choses, mais ici c'est différent :
Dans :
 ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
On a des opérateurs qu'on ne peut pas inverser :
)
et
)
et
)
parce qu'ils ne sont pas bijectives.
Par exemple, si on cherche à passer de :
 ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f)
à
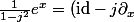 f)
, on a que :
 f \in \mathrm{ker} ( \mathrm{id} - j^2 \partial_x ) = \mathbb{R}. e^{jx})
, et après ?. Bref, je ne sais pas comment poursuivre ce travail seul.
Merci d'avance pour vos éclaircissements.
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 24 Fév 2015, 22:24
par SLA » 24 Fév 2015, 22:24
barbu23 a écrit:Oui, je sais, il faut que je compte sur moi même lorsqu'il s'agit de ce genre de choses, mais ici c'est différent :
Dans :
 ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f \\ ( \mathrm{id} - j \partial_x ) ( \frac{1}{1 - j^{2}} e^{jx} ) = ( \mathrm{id} - j \partial_x ) \circ ( \mathrm{id} - \partial_x ) f \\ ( \mathrm{id} - \partial_x ) ( \frac{1}{1 - j^{2}} e^{j^{2}x} ) = ( \mathrm{id} - \partial_x ) \circ ( \mathrm{id} - j^2 \partial_x ) f \end{cases})
On a des opérateurs qu'on ne peut pas inverser :
)
et
)
et
)
parce qu'ils ne sont pas bijectives.
Par exemple, si on cherche à passer de :
 ( \frac{1}{1 - j^{2}} e^x ) = ( \mathrm{id} - j^2 \partial_x ) \circ ( \mathrm{id} - j \partial_x ) f)
à
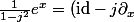 f)
, on a que :
 f \in \mathrm{ker} ( \mathrm{id} - j^2 \partial_x ) = \mathbb{R}. e^{jx})
, et après ?. Bref, je ne sais pas comment poursuivre ce travail seul.
Merci d'avance pour vos éclaircissements.
Oui, mais a défaut d'être bijectifs, on sait décrire le noyau de ces operateurs...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 23:05
par barbu23 » 24 Fév 2015, 23:05
On arrive donc, à l'expression :
 f \in \dfrac{1}{1 - j^{2}} e^x + \mathbb{R}. e^{j^{2}x})
Je ne sais pas ce qu'il faut faire exactement pour déterminer cette condition initiale pour :

, de façon à avoir :
 f = \dfrac{1}{1 - j^{2}} e^x)
. :triste:
Un petit indice !?!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Fév 2015, 23:18
par barbu23 » 24 Fév 2015, 23:18
On arrive donc, à l'expression :
 f \in \dfrac{1}{1 - j^{2}} e^x + \mathbb{R}. e^{j^{2}x})
Je ne sais pas ce qu'il faut faire exactement pour déterminer cette condition initiale pour :

, de façon à avoir :
 f = \dfrac{1}{1 - j^{2}} e^x)
. :triste:
Un petit indice !?!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
pour qu'on ait l'équivalence suivante :
et
et
parce qu'ils ne sont pas bijectives.
à
, on a que :
, et après ?. Bref, je ne sais pas comment poursuivre ce travail seul.