Composantes connexes !

par **barbu23** » 16 Déc 2009, 15:04

Non ce n'est pas un exo, mais c'est un passage d'un cours ecrit en anglais et qui dit que :
Theorem :
If

is an open set in

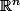
then for any embedding

the image

must be an open set in

.

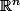
Proof:
Regarding

as the one-point compactification of

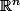
, an equivalent statement is that

; is open in

, and this is what we will prove. Each

is the center point of a disk

. It will suffice;ce to prove that

is open in

.
By the previous proposition

has two path-components. These path-
components are

and

, since these two subspaces are disjoint and the first is path-connected since it is homeomorphic to

while the second is path-connected by the proposition. Since

, is open in

, its path-
components are the same as its components. The components of a space with finitely many components are open, so

is open in

and hence also in

.

C'est à propos du theorème du domaine d'invariance de Brouwer ! :happy3:

par **Nightmare** » 16 Déc 2009, 15:06

Ok, c'est donc bien ce que proposait Angélique_64.

par **barbu23** » 16 Déc 2009, 16:21

Ok, merci ! :)

par **barbu23** » 16 Déc 2009, 16:49

On fait une petite synthèse :
Tout espace topologique se décompose en union disjointe de composantes connexes ! Dans notre cas, l'espace se decompose en un nombre fini disjoint de composantes connexes !
D'autre part, le complementaire d'une composante connexe quelconque, est la réunion de toutes les autres composantes connexes, qui sont toutes fermées et donc leur reunion est fermée ! Ce qui veut dire que la composante connexe est ouverte ( Donc, elle est à la fois ouverte et fermée, mais peu importe ) Par conséquent, reunion fini de composantes connexes ouvertes est ouverte, d'où l'espace est ouvert !
PS : "Ben314" , le signe :stupid_in n'était juste que pour rigoler un peu ! donc, ne le prends pas au serieux !

par **Nightmare** » 16 Déc 2009, 16:57

Oui, et c'est parce que la réunion est finie qu'on peut dire qu'elle est fermée !

par **SlowBrain** » 16 Déc 2009, 22:05

Euh... Salut les gars! Je me suis inscrit tout juste pour rappeler qu'une composante connexe d'un espace topologique (je vais l'appeler E parceque j'ai envie) est toujours ouverte ET fermée... Donc même un sous espace topologique qui serait l'union d'une giga-infinité plus que non dénombrable de composantes connexes serait un sous espace ouvert de E. Il vient d'où ce cours?

par **Nightmare** » 16 Déc 2009, 22:12

SlowBrain a écrit:Euh... Salut les gars! Je me suis inscrit tout juste pour rappeler qu'une composante connexe d'un espace topologique (je vais l'appeler E parceque j'ai envie) est toujours ouverte ET fermée... Donc même un sous espace topologique qui serait l'union d'une giga-infinité plus que non dénombrable de composantes connexes serait un sous espace ouvert de E. Il vient d'où ce cours?

Je ne suis pas d'accord ! Une composante connexe est fermée certes, mais pas forcément ouverte (dans l'espace de départ).

par **Ben314** » 16 Déc 2009, 22:13

Par exemple (par hasard) quoi c'est y que les composantes connexes de

muni de la topologie usuelle ?

par **Nightmare** » 16 Déc 2009, 22:13

Exemple : N et ses singletons.

par **Ben314** » 16 Déc 2009, 22:14

Là, j'ai peur .... que ce soit un mauvais exemple......

par **Nightmare** » 16 Déc 2009, 22:15

Pourquoi donc?

par **Ben314** » 16 Déc 2009, 22:17

Parce qu'il me semble que N est discret (pour la topo usuelle) et donc que toute partie est ouverte et fermée, en particulier les composantes connexes

par **Nightmare** » 16 Déc 2009, 22:18

Tu as raison, mais je n'ai pas précisé quelle topologie je mettais dessus. Cela dit je n'ai pas en tête de topologie qui me permettrait de te contredire :lol3:

par **Ben314** » 16 Déc 2009, 22:20

Je vais t'aider, comme N a le même cardinal que Q, tu peut transporter la topo de Q sur N via une bijection quelconque entre les deux....

En plus, les "nouvelles" composantes connexes sont... les singletons comme tu le précisait dans ton post. Ce qui prouve que c'est évidement à cette topologie que tu faisait alusion :zen:

par **Nightmare** » 16 Déc 2009, 22:25

Effectivement :happy3:

Cela dit, je me suis quand même lancé dans une topologie non "induite". En fait j'en connais une propre à N (entre autre, elle permet de démontrer par exemple l'infinitude des nombres premiers) : Un ensemble S est ouvert si pour tout n dedans, il existe une raison a pour laquelle la progression arithmétique de premier terme n soit contenue dans S, elle me semble marcher !

par **Doraki** » 16 Déc 2009, 22:26

Vous parlez de connexité par arc ou de connexité normale ? (E est connexe si les seules partie de E à la fois ouverte et fermée, sont E et l'ensemble vide)

par **Nightmare** » 16 Déc 2009, 22:27

Doraki a écrit:Vous parlez de connexité par arc ou de connexité normale ? (E est connexe si les seules partie de E à la fois ouverte et fermée, sont E et l'ensemble vide)

connexité normale pourquoi? Quelque chose te parait incorrect?

par **SlowBrain** » 16 Déc 2009, 22:28

zut oui, je me suis planté... c'est pour les localement connexe que les composantes connexes sont ouvertes et fermées... mais ça tombe bien Rn est localement connexe or c'est de lui qu'il s'agissait dans son document! Sinon, les composantes connexes de Q, ce sont bien les singletons? Ouf, personne n'a rien dit sur ma bêtise que j'ai écrite hier avant d'aller me coucher et que je suis en train d'éditer!!!!!! :briques:

par **Ben314** » 16 Déc 2009, 22:32

J'arrive pas encore à voir les composantes connexes dans ta topo, pour le moment j'ai juste que c'est pas séparé...

par **Nightmare** » 16 Déc 2009, 22:33

SlowBrain a écrit:zut oui, je me suis planté... c'est pour les localement connexe que les composantes connexes sont ouvertes et fermées... mais ça tombe bien Rn est localement connexe or c'est de lui qu'il s'agissait dans son document!

Oui, en fait c'est quasiment la définition d'un espace localement connexe !

Composantes connexes !

Qui est en ligne