Composantes connexes !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2009, 22:34
par Ben314 » 16 Déc 2009, 22:34
Nightmare, c'est quoi les composantes connexe pour "ta" topo sur N ?
Pour SlowBrain : les composantes connexe de Q sont les singletons (on dit qu'il est ??? discontinu : où ???=totalement ou extrèmement, je sais plus)
Je vient de chercher sur wikipédia : c'est "totalement discontinu"
il me semble que extrèmement discontinu c'est lorsque l'adhérence de tout ouvert est ouvert.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Déc 2009, 22:37
par Nightmare » 16 Déc 2009, 22:37
Ben314 > Après réflexion je pense qu'il ne marche pas. Déjà, les voisinages ouverts, ie les ensembles formées d'élément d'une même progression arithmétiques, sont aussi fermés.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Déc 2009, 09:29
par Ben314 » 17 Déc 2009, 09:29
Il me semble que les composantes connexes sont réduites à des points :
Si on note
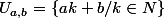
, alors, pour a fixé, les

avec

forment une partition de
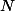
formée d'ouverts-fermés et, si X est une partie quelconque de
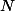
contenant plus de deux points, en regardant la trace de cette partition sur X (avec a bien choisi), on montre que X est non connexe...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Déc 2009, 16:45
par Nightmare » 17 Déc 2009, 16:45
Niquel, c'est donc que ça marche. Tu as donc réussi à te contredire tout seul :P

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Déc 2009, 17:21
par Ben314 » 17 Déc 2009, 17:21
Question : "ta" topologie est elle extrèmement discontinue (i.e. l'adhérence d'un ouvert est elle encore ouverte)
P.S. : Ce coup ci, c'est pas moi qui cherche... (j'ai des copies.....)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Déc 2009, 17:27
par Nightmare » 17 Déc 2009, 17:27
Si tu veux je prends les copies :lol3: (il est fou tu dois te dire)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Déc 2009, 18:27
par Nightmare » 17 Déc 2009, 18:27
Première remarque : deux ouverts ont forcément un point adhérent commun.
-
laquestion
- Membre Naturel
- Messages: 93
- Enregistré le: 07 Nov 2009, 16:42
-
 par laquestion » 17 Déc 2009, 22:59
par laquestion » 17 Déc 2009, 22:59
Nightmare a écrit:On peut éventuellement se poser la question dans l'autre sens : Si X est réunion d'ouverts (ou réunion finie de fermés) connexes, ces derniers sont-ils forcément des composantes connexes?
La réponse est trivialement oui, mais la question n'est pas inintéressante
la réunion des )-n,n( n entier non nul,donne R et aucun de ces intervalle connexe n'est une composante connexe de R...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Déc 2009, 23:01
par Nightmare » 17 Déc 2009, 23:01
Oui, j'ai oublié "disjointe" après "réunion" :happy.:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Déc 2009, 23:03
par Ben314 » 17 Déc 2009, 23:03
Je pense que Nightmare sous-entendait "...réunion disjointe de..."
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 18 Déc 2009, 00:26
par ffpower » 18 Déc 2009, 00:26
Barbu, ya un lien internet vers ton cours en anglais?Ca fait un moment que j'aimerais connaitre une preuve du theo d'invariance de Brouwer..
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Déc 2009, 12:13
par barbu23 » 18 Déc 2009, 12:13
Oui je sais : :happy3:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 18 Déc 2009, 19:02
par ffpower » 18 Déc 2009, 19:02
Ah, tu sais? tu m'espionne donc XD
Mais en l'occurence, pour le lien,c'est possible?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
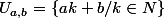 , alors, pour a fixé, les
, alors, pour a fixé, les  avec
avec  forment une partition de
forment une partition de 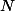 formée d'ouverts-fermés et, si X est une partie quelconque de
formée d'ouverts-fermés et, si X est une partie quelconque de 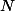 contenant plus de deux points, en regardant la trace de cette partition sur X (avec a bien choisi), on montre que X est non connexe...
contenant plus de deux points, en regardant la trace de cette partition sur X (avec a bien choisi), on montre que X est non connexe...