Non ce n'est pas un exo, mais c'est un passage d'un cours ecrit en anglais et qui dit que :
Theorem : If

is an open set in
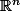
then for any embedding

the image
 $)
must be an open set in
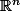
.
Proof: Regarding

as the one-point compactification of
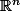
, an equivalent statement is that
 $)
; is open in

, and this is what we will prove. Each

is the center point of a disk

. It will suffice;ce to prove that
$)
is open in

.
By the previous proposition
 $)
has two path-components. These path-
components are
 $)
and
 $)
, since these two subspaces are disjoint and the first is path-connected since it is homeomorphic to

while the second is path-connected by the proposition. Since
 $)
, is open in

, its path-
components are the same as its components.
The components of a space with finitely many components are open, so
 $)
is open in
 $)
and hence also in

.
C'est à propos du theorème du domaine d'invariance de Brouwer ! :happy3:
