Complexes, similitudes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pionel
- Messages: 2
- Enregistré le: 01 Nov 2023, 09:31
-
 par Pionel » 01 Nov 2023, 09:51
par Pionel » 01 Nov 2023, 09:51
Bonjour,
Dans le cadre d'un devoir dont le but est de démontrer que les similitudes du plan complexes sont les applications de la forme z → az + b ou z → az¯ + b, je dois répondre à une question dont l'énoncé est le suivant :
On considère f une similitude de rapport 1 tel que f(0) = 0, f(1) = 1, f(i) = i. Montrer que pour tout z dans le cercle unité, f(z) = z (en passant par les formes trigos de f(z) et z)Tout d'abord, j'ai réussi à démontrer que f(z) et z possèdent le même module (en partant de |f(z) - f(0)| = |z - 0|) et je suis arrivé à f(z) = z ou f(z) = z¯ (en partant de |f(z) - f(1)| = |z - 1|, j'ai remplacé f(z) et z par leur forme trigo puis j'ai utilisé la technique de l'angle moitié pour aboutir à une égalité de sinus).
Je reste malheureusement bloqué à ce stade pour l'instant, c'est pourquoi je réclame votre aide !

Merci d'avance.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Nov 2023, 10:10
par Ben314 » 01 Nov 2023, 10:10
Salut,
On peut partir comme ça et dans ce cas, le fait qu'on doit aussi avoir
\!-\!i|\!=\!|f(z)\!-\!f(i)|\!=\!|z\!-\!i|)
va te dire que la solution est forcément
\!=\!z)
vu que, si
\!=\!\overline z)
alors
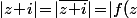\!-\!i|\!=\!|z\!-\!i|)
donc

est sur la médiatrice de
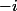
et

c'est à dire

est réel et
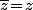
.
Sinon, je trouve que de procéder comme le demande l'énoncé avec du calcul et en commençant par le cercle trigo., c'est un peu concon : pour un z quelconque, vu les hypothèses, f(z) doit être situé sur les trois cercles passant par z et centré en 0, 1 et i. Et c'est pas bien compliqué de trouver des argument pour justifier que le seul point commun de ces trois cercles, c'est le point z donc qu'on a forcément f(z)=z.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pionel
- Messages: 2
- Enregistré le: 01 Nov 2023, 09:31
-
 par Pionel » 01 Nov 2023, 10:43
par Pionel » 01 Nov 2023, 10:43
Bonjour,
J'ai oublié de mentionner qu'en effet dans l'énoncé il est précisé que la démarche avec le cercle trigo. est inutile mais qu'il s'agissait ici de nous forcer à faire des manipulations avec des complexes. La piste que vous développez dans le second paragraphe est exactement la suite de l'énoncé de mon devoir

Merci beaucoup pour le déblocage et passez une agréable journée !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
