Salut!
Si a est un reel
J'ai vu dans le solution d'1 exo l'égalité suivante:
produit pr k variant de 0 à n-1 de (X-exp(i*(2k*Pi-a)/n) = produit pr k variant de 0 à n-1 de (X-exp(-i*(2k*Pi+a)/n)
?? d'ou vient cette égalité?
Merci
Complexes et racine n-ieme
3 messages
- Page 1 sur 1
par El_Gato » 12 Fév 2006, 16:03
Tu veux prouver que
}{n}}) = \prod_{k=0}^{n-1} (X - e^{\frac{-i(2k\pi + a)}{n}}))
.
Comme chaque}{n}} = e^{\frac{i2k\pi}{n}e^{\frac{-ia}{n}})
et de même }{n}} = e^{\frac{-i2k\pi}{n}e^{\frac{-ia}{n}})
tu es d'accord qu'il suffit de montrer:
 = \prod_{k=0}^{n-1} (X - e^{\frac{-i2k\pi}{n}}))
.
Mais cela est facile: les deux ensembles:
et 
sont en fait égaux. Pour k = 0 c'est évident. Ensuite par exemple pour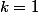 
:
\pi}{n}})
. Ainsi le terme correspondant à 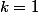du second ensemble correspond à celui de 
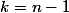du premier etc. et de même pour tous les autres k.
Comme chaque
Mais cela est facile: les deux ensembles:
par leibniz » 12 Fév 2006, 16:10
Oui, je confirme, en fait c'est ça la notion d'un groupe cyclique.
A+
A+
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :