Complexes et applications non affines
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 23 Déc 2018, 21:48
par checkmaths » 23 Déc 2018, 21:48
Bonjour, je suis en train de lire une correction d'exercice mais j'ai pas compris comment le correcteur a fait son compte pour trouver directement cette réponse à la question 3. En plus, ça fait depuis un moment que je cherche et je trouve pas, ça m'énerve

... Pourriez-vous m'aider svp


?
.\textrm{ On note }i\textrm{ le nombre comple-}\\\textrm{xe de module 1 et d'argument }\dfrac{\pi}{2}.\\\textrm{Soit }f\textrm{ l'application qui \`a tout point }m\textrm{ de }\mathcal{P}\textrm{ d'affixe }z\textrm{ }(z\neq-1),\textrm{ associe le point }M\textrm{ d'affixe :}\\\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;Z=\dfrac{z}{1+z}=1-\dfrac{1}{1+z}.\\\textbf{1)}\textrm{ D\'eterminer l'ensemble }D\textrm{ des points d'affixe }-\dfrac{3}{2}+iy\textrm{ }(y\in\mathbb{R}).\\\textcolor{white}{\textbf{1)}}\textcolor{blue}{\textrm{ L'ensemble }D\textrm{ des points d'affixe }z=-\dfrac{3}{2}+iy\textrm{ avec }y\in\mathbb{R}\textrm{ est la droite }D\textrm{ d'\'equation }x=-\dfrac{3}{2}.}\\\textbf{2)}\textrm{ Soit }z_1=z+1.\textrm{ Pr\'eciser la transformation g\'eom\'etrique }t_1\textrm{ qui associe \`a un point }m\textrm{ d'affixe }z,\\\textcolor{white}{\textbf{2)}}\textrm{ le point }M_1\textrm{ d'affixe }z_1.\\\textcolor{white}{\textbf{2)}}\textrm{ Quelle est l'image, not\'ee }D_1,\textrm{ de }D\textrm{ par la transformation }t_1\textrm{ ?}\\\textcolor{white}{\textbf{2)}}\textcolor{blue}{\textrm{ On note }t_1\textrm{ d\'efinie par }t_1(m)=M_1\textrm{ avec }z_1=z+1\textrm{ ; donc }t_1\textrm{ est la translation de vecteur }\vec{u}\textrm{ et}}\\\textcolor{white}{\textbf{2)}}\textcolor{blue}{\textrm{ }D_1\textrm{ est la droite d'\'equation }x=-\dfrac{1}{2}.}\\\textbf{3)}\textrm{ Soit }t_2\textrm{ la transformation g\'eom\'etrique qui au point d'affixe }z\textrm{ }(z\neq0)\textrm{ associe le point }M_2\textrm{ d'affi-}\\\textcolor{white}{\textbf{3)}}\textrm{ xe }z_2=\dfrac{1}{z}.\\\textcolor{white}{\textbf{3)}}\textrm{ Quelle est l'image, not\'ee }\mathit{\Gamma}_2,\textrm{ de }D_1\textrm{ par la transformation }t_2\textrm{ ?}\\\textcolor{white}{\textbf{3)}}\textcolor{blue}{\textrm{ On note }t_2\textrm{ d\'efinie par }t_2(m)=M_2\textrm{ avec }z_2=\dfrac{1}{z}\textrm{ et }z\neq0\textrm{ ; donc }t_2\textrm{ est l'inversion complexe et}}\\\textcolor{white}{\textbf{3)}}\textcolor{blue}{\textrm{ l'image de }\mathit{\Gamma}_2\textrm{ de }D_1\textrm{ est le cercle :}}\\\textcolor{white}{\textbf{3)}}\textcolor{blue}{\textrm{ -- de centre }\mathit{\Omega}(-1,0)\textrm{ car son affixe }z_{\mathit{\Omega}}=\dfrac{1}{2\times\left(-\frac{1}{2}\right)}=-1}\qquad\textcolor{red}{\textrm{ Je comprends pas cette formule...}}\\\textcolor{white}{\textbf{3)}}\textcolor{blue}{\textrm{ -- de rayon }R=\dfrac{1}{2\times\left|-\frac{1}{2}\right|}=1}\qquad\textcolor{red}{\textrm{Je comprends pas cette formule, non plus...}}\\\textcolor{white}{\textbf{3)}}\textcolor{blue}{\textrm{ priv\'e de }O.})
-
aviateur
 par aviateur » 23 Déc 2018, 23:01
par aviateur » 23 Déc 2018, 23:01
Bonjour
L'équation de

est z=-1/2+i y. Si tu sais que l'image de

est cercle privé de O (car 1/z tend vers 0 quand z tend vers l'infini), en tenant compte de la symétrie de

l'image est symétrique par rapport à Ox.
D'autre l'image de z=-1/2 est z=-2.
Le centre est alors le milieu de z=-2 et z=0, c'est le point d'affixe -1.
Evidemment le rayon est 1.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 23 Déc 2018, 23:19
par checkmaths » 23 Déc 2018, 23:19
Oui mais ça m'explique pas ces 2 formules... J'ai l'impression qu'elles sortent de nulle part... Pourquoi
}})
et
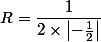
?
-
aviateur
 par aviateur » 23 Déc 2018, 23:31
par aviateur » 23 Déc 2018, 23:31
Et bien, perso je ne vois l'intérêt de connaître cette formule du fait qu'on la retrouve soi- même.
Si tu as une droite d'équation z=a+iy alors son image c'est le cercle privé de O
le point A d'affixe 1/a forme un diamètre avec O. Donc le centre à pour affixe 1/2(1/a) et le rayon c'est la valeur absolue.
Quand tu as une formule sortie de nulle part, tu la démontres et c'est tout.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 23 Déc 2018, 23:40
par checkmaths » 23 Déc 2018, 23:40
Ah ok d'accord je comprends mieux mtn merci bcp aviateur

Et passes un bon réveillon de Noël

-
aviateur
 par aviateur » 23 Déc 2018, 23:58
par aviateur » 23 Déc 2018, 23:58
Merci
Il sera au champagne!!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
 ... Pourriez-vous m'aider svp
... Pourriez-vous m'aider svp 
 ?
? ... Pourriez-vous m'aider svp
... Pourriez-vous m'aider svp 
 ?
?
