Complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Chercheuse
- Messages: 2
- Enregistré le: 27 Déc 2007, 07:55
-
par Chercheuse » 28 Déc 2007, 19:18
bonjour,
Pouvez vous m'aider a resoudre cet exercice
Exercice:
1) Calculer les racines quatrièmes de
. En déduire
et
2) Posons
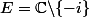
. Soit
quel que soit
.
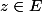
a) Monter que l'application
est injective.
b) Monter que pour tout
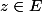
, on a
\neq0)
.
c) Démontrer l'égalité
=\mathbb{C}\backslash\{1\})
.
d) Soit
.
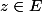
Montrer que
|^{2}=4\frac{\Im mz}{|z+i|^{2}}.)
e) Notons
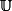
l'ensemble des nombres complexes de module 1. Montrer que l'on a
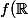=\mathbb{U}\backslash\{1\})
.
Pour 2) les questions a)-b) et d) sont faciles mais comment on démontre le c) et e)
Merci inifiniment.
-
bauzau
- Membre Relatif
- Messages: 189
- Enregistré le: 05 Jan 2007, 18:08
-
par bauzau » 29 Déc 2007, 11:51
aides-toi et le ciel t'aidera
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
par prody-G » 29 Déc 2007, 14:03
Pour la 2)c ça revient à montrer que f est surjective de E dans C\{1}.
Pour la d tu fais pareil, montre que f est surjective de R dans U\{1}, cad résoudre
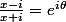
pour
non nul.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
