Complexe

[billy60]

Bonjour ! alors je tente de faire un exercice mais je bloque. Voice l'exercice :

On pose x=e^2i;)/5

1) calculer 1 + x + x^2 + x^3 + x^4. En déduire une équation de degré 2 en la variable Z=x + 1/x
2) Calculer cos(2;)/5) puis cos(;)/5)

Pour la question 1 j'ai essayé de factoriser par x ce qui donne x(1/x + 1 + x + x^2 + x^3) j'ai mis sur le même dénominateur
= x(1 + x + x^2 + x^3 + x^4/x) mais après je bloque :/
Pour la question 2 je pense utiliser les formules d'Euler donc voila pour la question 1 je suis preneur d'une quelconque aide

Merci d'avance

[siger]

bonjour

x= e^2 ln/5. sauf mauvaise lecture
""la variable Z = x+1/x " ??????
ou est la variable?

[billy60]

bonjour

x= e^2 ln/5. sauf mauvaise lecture
""la variable Z = x+1/x " ??????
ou est la variable?

Bonjour, alors non c'est x=e^2i;)/5 c'est un nombre complexe sous la forme exponentielle (avec =pi)
Concernant la variable je n'ai également pas compris la phrase c'est pour ça que je demande de l'aide mais je vous réécris la consigne

Posons x=e^2i;)/5
1) Calculons 1 + x + x^2 + x^3 + x^4. En déduire une équation de degré 2 en la variable Z=x + 1/x

[Robot]

Bonjour, alors non c'est x=e^2i;)/5 c'est un nombre complexe sous la forme exponentielle (avec =pi)
Concernant la variable je n'ai également pas compris la phrase c'est pour ça que je demande de l'aide mais je vous réécris la consigne

Posons x=e^2i;)/5
1) Calculons 1 + x + x^2 + x^3 + x^4. En déduire une équation de degré 2 en la variable Z=x + 1/x

Commençons par la première partie.

Que vaut ?
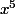
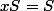
Soit . Montre que . Déduis-en la valeur de .

La suite de la question est mal formulée. On pourra mieux la reformuler quand on aura la valeur de .

[mathelot]

bonjour,

marche à suivre

i) la somme est celle d'une progression géométrique de raison x
après formulation, cette somme se révele nulle

ii) si
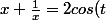On pose
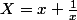
(du point de vue de l'analyse , c'est deux fois un cosinus)

calculer
factoriser dans la somme
remplacer cette équation par une équation en X de degré 2

[billy60]

Commençons par la première partie.

Que vaut ?
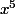
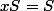
Soit . Montre que . Déduis-en la valeur de .

La suite de la question est mal formulée. On pourra mieux la reformuler quand on aura la valeur de .

- x^5= (e^2i;)/5)^5=(e^10i;)/5)=(e^5i;))
- xS= x(1+x+x^2+x^3+x^4)=x+x^2+x^3+x^4+x^5 ? Mais comment déduire la valeur de S alors que vous me dites que S=(1+x+x^2+x^3+x^4)

[Robot]

(e^10i;)/5)=(e^5i;))

Hum hum ....

[billy60]

Hum hum ....

Oops c'est (e^10i;)/5)=(e^2i;))

[Robot]

Et , ça ne te dit rien ?
Faudrait peut-être revoir un peu tes cours ...

[billy60]

Et , ça ne te dit rien ?
Faudrait peut-être revoir un peu tes cours ...

Si e^2i;)=1 j'ai compris merci beaucoup par contre j'ai toujours pas compris votre idée de xS=S (bien que j'ai compris comment résoudre la moitié de la question 1)

[MouLou]

Bin que vaut S si xS=S?