Complexe aide

[Anne33]

Pour un nombre complexe z différent de i on pose: w=(z+i)/(z-i)

1) si z est réel, quel est le module de w?
2)Montrer que si z est de module 1, alors w est un imaginaire pur.

je ne sais pas comment je dois faire.

[capitaine nuggets]

Pour un nombre complexe z différent de i on pose: w=(z+i)/(z-i)

1) si z est réel, quel est le module de w?
2)Montrer que si z est de module 1, alors w est un imaginaire pur.

je ne sais pas comment je dois faire.

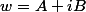
1) Supposons réel, écris sous forme algébrique (écris-le sous la forme , où et sont réels).
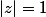
2) Remarque que si et seulement s'il existe tel que .

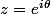
[Carpate]

Pour un nombre complexe z différent de i on pose: w=(z+i)/(z-i)

1) si z est réel, quel est le module de w?
2)Montrer que si z est de module 1, alors w est un imaginaire pur.

je ne sais pas comment je dois faire.

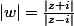
Si z est réel, quelle relation existe-t-il entre |z+i| et |z-i| ?

[Anne33]

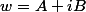
1) Supposons réel, écris sous forme algébrique (écris-le sous la forme , où et sont réels).
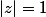
2) Remarque que si et seulement s'il existe tel que .

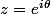
1)z=a+ib or z est réel alors z=a car b=0 donc w=(a+i)/(a-i) donc |w|= |a+i|/|a-i|
je me retrouve avec le module des conjugués et |z barre|=|z| donc |w|=1?

[Anne33]

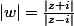
Si z est réel, quelle relation existe-t-il entre |z+i| et |z-i| ?

|z+i| = |z-i| et |w|=1

[Carpate]

|z+i| = |z-i| et |w|=1

Oui et pour la question 2 ?

[zygomatique]

Pour un nombre complexe z différent de i on pose: w=(z+i)/(z-i)

1) si z est réel, quel est le module de w?
2)Montrer que si z est de module 1, alors w est un imaginaire pur.

je ne sais pas comment je dois faire.

salut

si z est réel alors z + i et z - i sont conjugués or .... donc ....

si |z| = 1 alors multiplier numérateur et dénominateur de w par (z* + i) ....

où z* est le conjugué de z ...


:zen:

[Anne33]

Oui et pour la question 2 ?

Pour la 2) j'arrive à w=((exponentielle i téta) +1)/ ((exponentielle i téta)-1) et je bloc!!! :hein:

[zygomatique]

Pour la 2) j'arrive à w=((exponentielle i téta) +1)/ ((exponentielle i téta)-1) et je bloc!!! :hein:

normal ... vu que c'est compliqué ....

je t'ai proposé autre chose qui permet de répondre quasi immédiatement ....

[Anne33]

salut

si z est réel alors z + i et z - i sont conjugués or .... donc ....

si |z| = 1 alors multiplier numérateur et dénominateur de w par (z* + i) ....

où z* est le conjugué de z ...


:zen:

Pour faire ceci je dois passer sous forme trigo? ou algébrique?

[Anne33]

normal ... vu que c'est compliqué ....

je t'ai proposé autre chose qui permet de répondre quasi immédiatement ....

je trouve w= -(i cos téta)/(1-sin téta)

[Carpate]

je trouve w= -(1+sin téta)/(i cos téta)

Si tu suis la méthode de zygomatique, tu obtiendras au numérateur
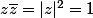
Or , donc il reste au numérateur :
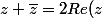donc numérateur imaginaire pur
Au dénominateur :
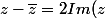donc réel
Conclusion ....

[Anne33]

Si tu suis la méthode de zygomatique, tu obtiendras au numérateur
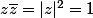
Or , donc il reste au numérateur :
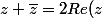donc numérateur imaginaire pur
Au dénominateur :
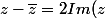donc réel
Conclusion ....

ok merci je pensais qu'il faillait transformer z.

[zygomatique]

attention il y a une petite erreur ::

z - z* = 2iIm(z) donc i(z - z*) est réel ainsi que 2 + i(z - z*)

donc le dénominateur est réel et le numérateur est imaginaire pur ....

d'où al conclusion attendue ....