Complétude polynôme d'Hermite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
par Mathusalem » 16 Mai 2012, 09:34
Bonjour,
L'expression (à la physicienne) du polynôme d'hermite est comme suit
 = (-1)^n e^{x^2}\frac{d}{dx^n}e^{-x^2})
La solution du problème à valeurs propres de l'oscillateur harmonique (en méca quantique)
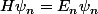
a pour solution
 = \sqrt{\frac{1}{2^nn!\sqrt{\pi}}}H_n(x)e^{-\frac{x^2}{2}})
J'ai déjà montré l'orthonormalité de ces solutions par
 := \int \limits_{-\infty}^{\infty} \psi_n(x)\psi_m(x) dx = \delta_{nm})
Et je dois montrer la complétude (?) de ces solutions, c'est-à-dire
\psi_n(x') = \delta(x-x'))
On me conseille d'utiliser dans l'expression du polynôme d'Hermite la représentation en séries de Fourier de la gaussienne. Donc si mes souvenirs sont bons, je peux écrire
 \psi_n(x') = \frac{1}{2^nn!\sqrt{\pi}}e^{\frac{x^2}{2}}\frac{d}{dx^n}\left[\int \limits_{-\infty}^{\infty} \frac{1}{2\pi}e^{-2p^2}e^{-ixp}dp\right]e^{\frac{x'^2}{2}}\frac{d}{dx'^n}\left[\int \limits_{-\infty}^{\infty} \frac{1}{2\pi}e^{-2p'^2}e^{-ix'p'}dp'\right])
Mais ça m'avance pas trop...
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 17 Mai 2012, 21:28
Mathusalem a écrit:Bonjour,
L'expression (à la physicienne) du polynôme d'hermite est comme suit
La solution du problème à valeurs propres de l'oscillateur harmonique (en méca quantique)
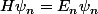
a pour solution
J'ai déjà montré l'orthonormalité de ces solutions par
Et je dois montrer la complétude (?) de ces solutions, c'est-à-dire
On me conseille d'utiliser dans l'expression du polynôme d'Hermite la représentation en séries de Fourier de la gaussienne. Donc si mes souvenirs sont bons, je peux écrire
Mais ça m'avance pas trop...
Bonsoir.
Que penses-tu de quelques bonnes grosses intégrations par parties ?
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
par Mathusalem » 17 Mai 2012, 23:23
ev85 a écrit:Bonsoir.
Que penses-tu de quelques bonnes grosses intégrations par parties ?
Dans le genre rentrer la dérivée dedans et intégrer du
^2} dp)
?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 18 Mai 2012, 06:28
Mathusalem a écrit:Dans le genre rentrer la dérivée dedans et intégrer du
?
Hmmm. Je suis allé un peu vite me semble-t-il; ça serait pour montrer que
=\delta_{m,n})
mais ça tu l'as fait depuis longtemps je parie...
Par ailleurs ce que tu as écrit ressemble plus à des transformées de Fourier qu'à des séries de Fourier.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
