Complétude ou non complétude

[Lostounet]

Salut,

Je dois montrer que l'espace est complet pour la norme et mais pas pour la norme

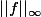
Il faut dire que je ne suis pas encore à l'aise avec mon cours: mais je sais au moins qu'un espace est complet si toute suite de Cauchy est convergente...

[Robot]

Tu peux déjà voir le contre-exemple : une suite de fonctions C^1 qui converge uniformément sur [0,1] vers une fonction non C^1 ?

[jlb]

Salut, je pense pouvoir t'aider: considère une suite (fn_n) de Cauchy de ton espace.

Traduis d'abord cela pour le norme utilisée

[Lostounet]

Zygomatique a dit ça sur mon autre fil :

salut

un exemple simple de fonction C1 qui ne converge pas dans C1([0, 1], R) :

on a évidemment pour tout n ::

et pour tout x 0

donc sa limite n'est pas continue ....




on remarquera que les f_n sont bornées ....

Qu'en penser pour la norme infinie...

Salut, je pense pouvoir t'aider: considère une suite (fn_n) de Cauchy de ton espace. Traduis d'abord cela pour le norme utilisée

Pourquoi tu as plusieurs n dans ta suite.

Bon je suppose que (fn) est une suite de Cauchy...
N(f) = comme somme de deux sup?

En fait je peux réécrire f(x) en fonction de f':

[jlb]

Zygomatique a dit ça sur mon autre fil :


Qu'en penser pour la norme infinie...



Pourquoi tu as plusieurs n dans ta suite.

Bon je suppose que (fn) est une suite de Cauchy...
N(f) = comme somme de deux sup?

En fait je peux réécrire f(x) en fonction de f':

désolé, j'ai fait une erreur de frappe!

Traduis que (f_n) est une suite de Cauchy à partir de la définition et pour la norme envisagée.
Ton exemple ne va pas, on souhaite une suite convergent uniformément.( ce n'est pas ton cas, la fonction limite devrait être continue!)
Tu peux considérer la suite de fonctions (x+1/n²)^0,5

[Lostounet]

désolé, j'ai fait une erreur de frappe!

Traduis que (f_n) est une suite de Cauchy à partir de la définition et pour la norme envisagée.
Ton exemple ne va pas, on souhaite une suite congervent uniformément.( ce n'est pas ton cas, la fonction limite devrait être continue!)

Soit (fn) une suite de Cauchy. Je cherche à montrer que toute suite de Cauchy va converger dans l'espace c'est bien ça?

Alors:



Je dois travailler sur = ?

[jlb]

Soit (fn) une suite de Cauchy. Je cherche à montrer que toute suite de Cauchy va converger dans l'espace c'est bien ça?

Alors:



Je dois travailler sur = ?

C'est cela! écris maintenant ce que signifie les expressions avec les normes et pense à cela: si deux quantités positives sont plus petites qu'un nombre, que peux-tu dire de chacune d'entre elles?

PS: je t'ai proposé un exemple dans le message précédent ( regarde la limite simple et il te restera à montrer que la cv est uniforme)

[Lostounet]

C'est cela! écris maintenant ce que signifie les expressions avec les normes et pense à cela: si deux quantités positives sont plus petites qu'un nombre, que peux-tu dire de chacune d'entre elles?

PS: je t'ai proposé un exemple dans le message précédent ( regarde la limite simple et il te restera à montrer que la cv est uniforme)

Les (fn) sont bien de classe C1 sur [0;1] alors que la fonction racine carrée n'est pas C1 dessus !

Revenons donc à l'étude de la norme:




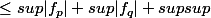
Je peux dire que la quantité positive est majorée par la somme des sup par l'inégalité triangulaire...

[jlb]

Bon tu pars mal, écris plutôt que ce que l'inégalité de départ implique que
ET

Ensuite, on va travailler pour chaque inégalité de la même manière:

l'objectif c'est d'obtenir la convergence vers une fonction f C1.
on n'a pas f pour l'instant, on va la construire point par point

Traduis la première inégalité avec "des x" pour faire apparaître des "f_p(x) et f_q(x)" pour travailler dans R qui est complet.

PS1:( et pour ton autre post, regarde la tête des projections, il n'y a pas une norme plus adaptée que les autres?)
PS2: il te rste à montrer que la convergence est uniforme pour l'exemple, cela utilise des propriétés de la fct racine carrée

[Lostounet]

[quote="jlb"]Bon tu pars mal, écris plutôt que ce que l'inégalité de départ implique que
[TEX]
N(f_p - f_q)_\infty N1,
N(fp(x) - fq(x)) < epsilon par complétude de R

edit: Oui: On a bien convergence simple vers la fonction racine de x, notée f, puis je montre que:
|fn - f| = (V(x + 1/n^2) - Vx)
puis j'ai multiplié par le conjugué

edit2: une norme plus adapté.. je regarde

[jlb]

Tu as l'idée mais tu t'emballes ( déroule ce que tu as sous la main jusqu'au bout): on a en traduisant la première inégalité pour tout x de [0,1] |f_q(x)-f_p(x)|< epsilon dès que p,q>N

Du coup pour un x choisi dans [0,1] la suite (f_n(x) est de Cauchy dans R donc convergente vers un nombre f(x).
Ceci étant vrai pour tous les x de [0,1], on a notre fonction limite f!! youpi!!

Reste à montrer qu'elle est C1

Pour ç on repart de notre inégalité: à epsilon fixé quelconque, à x fixé quelconque on fait tendre p vers plus l'infini comme la valeur absolue est continue, tu obtiens que

pour notre epsilon, il existe N entier tel que pour tout q>N pour tout x dans [0,1] |f_q(x)-f(x)|
Tu as donc la convergence uniforme de (f_n) vers f et comme les f_n sont continues tu sais que...

[Lostounet]

Je commence un peu à comprendre. Je crois.

Mais du coup c'est pas la dérivabilité qu'on vise? Et ensuite la continuité des (f'_n) en deuxième manche?

[jlb]

Je commence un peu à comprendre. Je crois.

Mais du coup c'est pas la dérivabilité qu'on vise? Et ensuite la continuité des (f'_n) en deuxième manche?

Bon on vient de montrer que f est continue, je te laisse finir!! on n'a pas encore utliser la deuxième inégalité avec la suite (f'_n)
étape 1: elle converge uniformément vers une fonction g continue ( même raisonnement)
étape 2: g=f' ( relis ton cours sur les séries de fct et leur dérivabilité)

Bon courage, je dois allez travailler, je peux regarder ce soir si tu as des soucis ( après essaie en relisant ton cours sur les séries de fct et dérivabilité d'optimiser l'explication.

pour la cv uniforme de l'exemple tu vas peut-être pas conclure avec la quantité conjuguée (en fait si!!) tu peux aussi dire que rac(x)=<rac(x+1/n²) croissance de fct racine et rac(x+1/n²)=<rac(x) +1/n ( propriété utile rac(a+b)=<rac(a)+rac(b) à démontrer) donc |rac(x+1/n²)-rac(x)|=<1/n

[Lostounet]

Je viens de relire mon cours sur la convergence uniforme et la classe C1.
En fait il y a trois points que je dois vérifier:

* la suite (fn) est C1 sur [0; 1]
* la suite des (f'n) converge uniformément vers g
* il existe a tel que (fn(a)) possède une limite finie (je prends a = 0..) L

Alors la suite fn converge uniformément vers la fonction limite f de classe C1 et telle que f' = g, f(a) = L

Du coup, j'ai bien le premier point trivialement car c'est toutes des fonctions C1.

Montrons que la suite des dérivées converge uniformément...Est-ce que c'est ce que tu as fait?

Car dans ton dernier post tu bosses sur la convergence uniforme de f, alors que je crois que ce serait mieux de travailler sur les f' pour récupérer la classe C1.

[jlb]

Je viens de relire mon cours sur la convergence uniforme et la classe C1.
En fait il y a trois points que je dois vérifier:

* la suite (fn) est C1 sur [0; 1]
* la suite des (f'n) converge uniformément vers g
* il existe a tel que (fn(a)) possède une limite finie (je prends a = 0..) L

Alors la suite fn converge uniformément vers la fonction limite f de classe C1 et telle que f' = g, f(a) = L

Du coup, j'ai bien le premier point trivialement car c'est toutes des fonctions C1.

Montrons que la suite des dérivées converge uniformément...Est-ce que c'est ce que tu as fait?

Car dans ton dernier post tu bosses sur la convergence uniforme de f, alors que je crois que ce serait mieux de travailler sur les f' pour récupérer la classe C1.

Bon tu vas plus vite que la musique mais si tu t'en souviens ensuite ce sera Ok.

Logiquement, si tu dois montrer que f est C1 c'est bien de vérifier que f est continue, puis f est dérivable et à dérivée continue: c'était la première partie de mon message ( en t'inspirant de la méthode pour la continuité, tu aurais montré la cv uniforme de (f'_n) et la dérivabilité et la continuité)

Ensuite je t'ai annoncé qu'il y avait plus rapide, en utilisant le théorème que tu cites: il y a moins de boulot!! et du coup tu n'as plus qu'à adapter pour (f'_n) ce qu'on a fait pour (f_n) et la convergence simple de (f_n) ( début de ce qu'on a fait))
C'était uniquement pour t'entrainer au raisonnement, rédige comme tu veux ensuite et au plus rapide!!
Bon courage.

[MouLou]

Oui tu as raison Lostounet de mon point de vue qui est le suivant:

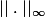
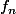
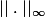
au cours de ses pistes, Jlb t'a fait montrer que l'espace C([0,1],R) est complet pour . ie que tout suite de fonction continue qui est de cauchy pour converge uniformément vers une fonction continue.

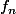
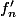
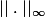
Donc si tu prends une suite de Cauchy pour ta norme N( qui prend en compte la norme infinie de la dérivée), alors les suites et sont de cauchy pour . Donc en utilisant la complétude et le théorème de dérivabilité des limites uniformes de fonction C1, tu devrais pouvoir conclure.

J espere que l'interférence d'explications va pas trop t'embrouiller

[Lostounet]

Je vous remercie, Jlb et MouLou. Je vais essayer et je vous dit.

Au passage Jlb, non je ne m'en souviendrais pas :ptdr: Je n'arrive pas à retenir les 50 hypothèses de chaque théorème sur les classe C^k.. (surtout celles des intégrales à paramètre :cry: )

[MouLou]

Ca viendra tkt, faut juste les appliquer encore et encore

[Lostounet]

MouLou, il y a un pb... C'est dans l'espace des fonctions C1 qu'on travaille, pas continues tout court.
Et la suite (fn) = (x + 1/n^2)^2 est C1 mais converge vers la fonction racine qui n'est pas de classe C1 sur [0; 1] ... donc je vois pas comment c'est complet pour la norme infinie toute seule...

[jlb]

Moulou a dit: C([0;1],R) est complet pour la norme infinie, il a pas dit C1([0;1],R) et comme tu pars d'une suite de fctions C1, leur dérivées sont dans C([0;1],R)