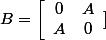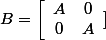Comparer deux spectres

[Fox123]

Bonjours à tous.

Je prépare les oraux et je suis resté bloqué sur un exo:

Soit A appartenant à Mn(R) et B une matrice par bloque B=[[0,A],[transp(A),0]]

Comparer les spectres de B et transp(A)A.



Je ne vois pas comment commencer, j'ai essayé avec une matrice 2X2 mais ca ne donne rien...

Merci d'avance pour toute indication.

[Doraki]

Tu as cherché à quoi peuvent ressembler des vecteurs propres de B ?

[Fox123]

en prenant le cas A 2X2 et X vecteur propre, X=(x1,x2,x3,x4), µ valeur propre:

µX= [[A(x3,x4)],[transp(A)(x1,x2]]

[Doraki]

oui, donc, matriciellement, t'en déduis quoi comme relations entre (x1,x2), (x3,x4), mu, A, et tA ?

[fourize]

bonjour tout les deux !

je n'arrive pas à comprendre comment B en vrai :doh: mais on fera avec lol

*d'abord si B s'ecrit comme ça:

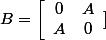
le spectre de B sera nul; et donc différant de A.

* si B s'ecrit comme ça:

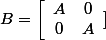
le spectre de B sera le double de celle de A : i.e spectre(B)> spectre(A)

je pense etre bien clair !

[Fox123]

B s'écrit comme ca:


@ Doraki: j'ai sorti le brouillon, je te dis quand j'ai trouvé.

EDIT: µ(x1,x2)=A(x3,x4) et µ(x3,x4)=t(A)(x1,x2)

ca a l'air pas trop mal, je vais essayer de conclure...

[Fox123]

la première équation me dit que si µ est valeur propre commune xi=xj quelque soit i et j.
par contre je ne vois pas ce qu'apporte la seconde.

[Doraki]

En posant X=(x1,x2) et Y=(x3,x4), on a bien µX = A.Y et µY = tA.X

On ne te demande pas de chercher un lien entre mu et une valeur propre de A, mais plutot avec une valeur propre de AtA.
Prises séparément, les deux équations n'apportent absolument rien du tout.

[Fox123]

ok, donc µ²Y=t(A)AY et quelque soit µ dans Sp(B) µ² est dans Sp(tAA).

J'ai bon?

[Doraki]

Oui sauf que t'as transformé tA.A en A sans raison.

[Fox123]

oups oui, édité.

Merci beaucoup pour ton aide!