Comparaison de suites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
doc123
- Membre Naturel
- Messages: 37
- Enregistré le: 11 Oct 2007, 20:57
-
 par doc123 » 25 Jan 2009, 20:37
par doc123 » 25 Jan 2009, 20:37
Bonsoir;
J'ai un petit problème à résoudre: Merci de votre aide:
On pose cette suite:
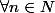
=\sum_{k=0}^n \frac{x^k}{k !})
1) commet peut on comparer les deux réels suivant:
j'ai pensé à les equivalents mais je ne suis pas sur;

et
)
---> k parmi n
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 25 Jan 2009, 21:03
par Clembou » 25 Jan 2009, 21:03
doc123 a écrit:Bonsoir;
J'ai un petit problème à résoudre: Merci de votre aide:
On pose cette suite:
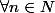
=\sum_{k=0}^n \frac{x^k}{k !})
1) commet peut on comparer les deux réels suivant:
j'ai pensé à les equivalents mais je ne suis pas sur;

et
)
---> k parmi n
Heu ! Rien capté :triste:
Les deux réels qui faut comparer c'est

et
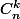
???
-
doc123
- Membre Naturel
- Messages: 37
- Enregistré le: 11 Oct 2007, 20:57
-
 par doc123 » 25 Jan 2009, 21:07
par doc123 » 25 Jan 2009, 21:07
oui, c'est sa
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 25 Jan 2009, 21:09
par Clembou » 25 Jan 2009, 21:09
Ba d'un côté tu as

et de l'autre tu as :
!k!})
....
Qu'est ce que tu peux en dire ???
-
doc123
- Membre Naturel
- Messages: 37
- Enregistré le: 11 Oct 2007, 20:57
-
 par doc123 » 25 Jan 2009, 21:13
par doc123 » 25 Jan 2009, 21:13

< 0
et C

est un entier non ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 25 Jan 2009, 21:19
par Clembou » 25 Jan 2009, 21:19
Mieux. Si tu fais :

qu'est ce que ça donne ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 25 Jan 2009, 21:24
par yos » 25 Jan 2009, 21:24
Sinon

.
Ca c'est du large!
-
doc123
- Membre Naturel
- Messages: 37
- Enregistré le: 11 Oct 2007, 20:57
-
 par doc123 » 28 Jan 2009, 19:42
par doc123 » 28 Jan 2009, 19:42
Bonjour , YOS
comment peut on démontrer le résultat obtenu ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 28 Jan 2009, 21:20
par yos » 28 Jan 2009, 21:20
L'encadrement

?
C'est évident non?
1 divisé par un entier, ça doit bien être plus petit que 1.
Quant à
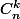
, c'est un entier strictement positif.
-
doc123
- Membre Naturel
- Messages: 37
- Enregistré le: 11 Oct 2007, 20:57
-
 par doc123 » 28 Jan 2009, 23:22
par doc123 » 28 Jan 2009, 23:22
merci, pour ce détail
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités