Un compact

[Houuda]

bonsoir
svp dans quel espace on peut dire qu'une partie bornée fermée est un compact ? Mercii :)

[Sylviel]

Dans un espace de dimension finie. En dimension infinie la boule unité n'est pas compacte.

[Archytas]

Il me semble que plus généralement on appelle ça les espaces de Daniell ! Donc les espaces de dimension finie sont en effet des espaces de Daniell mais y en a d'autres.

[bolza]

Bonjour,

je m'intéresse justement aux conditions minimales que doit vérifier un espace topologique pour que
"fermé borné" <-> "compact".

Auriez vous une (ou des) références à propos des espaces de Daniell ?

[Ben314]

Salut,
Juste un "petite" remarque : si tu t'intéresse comme tu le dit aux espaces topologiques, la notion de "dimension" est très floue (il y a des tas de définitions possibles) et celle de "partie bornée" est inexistante.
Donc...

[bolza]

Oui, on a besoin d'une métrique pour que "borné" ait un sens.
Donc être dans un espace métrique est nécessaire, mais ce n'est pas suffisant.

Pour la notion de dimension, en a t-on vraiment besoin ?
certes être dans un espace vectoriel de dimension fini est suffisant,
mais est-ce vraiment nécessaire ?

et encore est-ce vrai pour tout les espaces vectoriels ?
parce que par exemple si on prend simplement le cas de ,
toutes les preuves que j'ai trouvé que les "fermés bornés de " sont compact
utilisent à un moment ou un autre (souvent de manière implicite) que est complet.

Cette hypothèse de complétude est utilisée seulement pour des raisons pratiques
parque ça simplifie la preuve, ou parce qu'on en a vraiment besoin ?

Autrement dit si on prend l'exemple de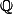 (qui est un 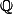-espace vectoriel de dimension fini).
Les fermés bornés de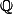 sont-ils compact ?

je pense que non, car si je prend une suite dans un fermé borné de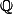
qui converge vers un irrationel, alors cette suite n'a aucune sous-suite convergente
dans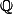 , donc l'ensemble n'est pas compact.

Donc on aurait besoins d'un espace métrique complet qui vérifierait d'autres propriétés.

Pour en revenir aux espaces vectoriels de dimension fini,
est-ce la dimension fini qui est importante ?
ou bien est-ce une autre propriété qui est vérifié par les espaces vectoriels de dimension fini
et que l'on perd quand on passe en dimension infini ?

[arnaud32]

vu qu'un compact est necessairement complet oui je pense qu'il te faut (X,d) metrique complet

[jlb]

Autrement dit si on prend l'exemple de (qui est un -espace vectoriel de dimension fini).
Les fermés bornés de sont-ils compact ?

je pense que non, car si je prend une suite dans un fermé borné de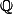
qui converge vers un irrationel, alors cette suite n'a aucune sous-suite convergente
dans , donc l'ensemble n'est pas compact.

Donc on aurait besoins d'un espace métrique complet qui vérifierait d'autres propriétés.

Bonjour, je ne suis pas doué, ce passage est-il juste?

Une autre question: j'ai appris le théorème de Riez pour des espaces vectoriels normés ( sur R ou C), ce théorème est-il valable pour d'autres e.v.n? sous d'autres conditions?

Merci si vous pouvez m'éclairer.

[bolza]

Bonjour, jlb

pour le passage auquel tu fais référence, j'utilise le théorème de Bolzano-Weierstrass qui dit que
dans un espace topologique, est compact ssi toute suite à valeur dans admet une valeur d'adhérence.

Pour ce qui est du théorème de Riesz, il me semble que tout espace vectoriel normé de dimension fini
est isomorphe à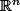 (à vérifier).

[Godfrey]

[...] si je prend une suite dans un fermé borné de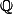
qui converge vers un irrationel, alors cette suite n'a aucune sous-suite convergente
dans , donc l'ensemble n'est pas compact.

Je ne suis pas certain de ta preuve. Si tu as une suite dans ton fermé borné qui converge, sa limite est nécéssairement dans ce fermé.
Par conséquent, tu ne peux pas te donner une telle suite convergeant vers un irrationnel.

[Godfrey]

Pour ce qui est du théorème de Riesz, il me semble que tout espace vectoriel normé de dimension fini
est isomorphe à (à vérifier).

C'est clair, après avoir choisi une base !

[mathelot]

Bonjour, jlb

j'utilise le théorème de Bolzano-Weierstrass qui dit que
dans un espace topologique métrisable, est compact ssi toute suite à valeur dans admet une valeur d'adhérence.

vous êtes certain ? quid des e.v.t non métrisables ou n'admettant
pas une base dénombrable de voisinages ? Notamment pour les espaces de fonctions,
la topologie de la convergence ponctuelle n'est pas métrisable.

[paquito]

Il y a une définition pour les espaces métriques (de toute suite à valeurs dans K, on peut extraire une sous suite convergente) et la définition générale pour les espaces topologiques (de tout recouvrement fermé de K on peut extraire un sous recouvrement fini); il en résulte que tout fermé inclus dans un compact est compact. Donc Sylviel t'a donné la réponse.

[paquito]

Un exemple de boule unité non compacte.

On se place dans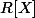avec si ,et soit une suite incluse dans la sphère unité S; S, image réciproque du fermé {1} par une application continue est fermée et trivialement bornée; mais||P_i-P_j||=1 chaque fois que ; par conséquent, on ne peut extraire de aucune sous suite de Cauchy et a fortiori aucune sous suite convergente.

[bolza]

Soyons précis dans les définition :

Définition de compact : Dans un espace topologique quelconque, K est compact ssi de tous recouvrements
par des ouverts, on peut en extraire un sous-recouvrement fini.

après il y a un théorème :

Dans un espace topologique quelconque (oui, oui, quelconque ;p (... bon d'accord, peut être séparé)) :
K est compact ssi toutes suites à valeur dans K admet une valeur d'adhérence.

Ensuite deuxième propriété : Dans un espace métrique (ou métrisable) les valeurs d'adhérences d'une suite
sont les limites de ses sous-suite.

Avec ça on démontre que dans un espace métrique :
K compact <-> toutes suites à valeur dans K admet une sous-suite convergente.

Ensuite les propriétés :
i) compact => fermé
ii) fermé et inclus ds un compact => compact

sont vrai dans un espace topologique quelconque.

Dans un espace métrique, on peut montrer de plus que compact => borné.
donc dans un espace métrique on a compact => fermé borné

Maintenant intéressons nous à la réciproque.
Certes dans les evn de dimension fini fermé borné => compact.
Mais est-ce vraiment nécessaire d'être dans un evn ?
Autrement dit existe-il quelque chose qui ne soit pas un espace vectoriel et pour lequel
fermé borné => compact ?
ou a-t-on réellement besoin de toute la structure d'espace vectoriel pour avoir fermé borné => compact ?

En faite ce qui m'interpelle, c'est que pour la réciproque on ait besoin d'avoir des hypothèses aussi fortes.

N.B. : pour certain résultat que j'ai annoncé je crois que l'espace topologique doit être séparé

[paquito]

Soyons précis dans les définition :

Définition de compact : Dans un espace topologique quelconque, K est compact ssi de tous recouvrements
par des ouverts, on peut en extraire un sous-recouvrement fini.

après il y a un théorème :

Dans un espace topologique quelconque (oui, oui, quelconque ;p (... bon d'accord, peut être séparé)) :
K est compact ssi toutes suites à valeur dans K admet une valeur d'adhérence.

Ensuite deuxième propriété : Dans un espace métrique (ou métrisable) les valeurs d'adhérences d'une suite
sont les limites de ses sous-suite.

Avec ça on démontre que dans un espace métrique :
K compact toutes suites à valeur dans K admet une sous-suite convergente.

Ensuite les propriétés :
i) compact => fermé
ii) fermé et inclus ds un compact => compact

sont vrai dans un espace topologique quelconque.

Dans un espace métrique, on peut montrer de plus que compact => borné.
donc dans un espace métrique on a compact => fermé borné

Maintenant intéressons nous à la réciproque.
Certes dans les evn de dimension fini fermé borné => compact.
Mais est-ce vraiment nécessaire d'être dans un evn ?
Autrement dit existe-il quelque chose qui ne soit pas un espace vectoriel et pour lequel
fermé borné => compact ?
ou a-t-on réellement besoin de toute la structure d'espace vectoriel pour avoir fermé borné => compact ?

En faite ce qui m'interpelle, c'est que pour la réciproque on ait besoin d'avoir des hypothèses aussi fortes.

N.B. : pour certain résultat que j'ai annoncé je crois que l'espace topologique doit être séparé

désolé, je n'ai même pas vérifié!

[paquito]

Soyons précis dans les définition :

Définition de compact : Dans un espace topologique quelconque, K est compact ssi de tous recouvrements
par des ouverts, on peut en extraire un sous-recouvrement fini.

après il y a un théorème :

Dans un espace topologique quelconque (oui, oui, quelconque ;p (... bon d'accord, peut être séparé)) :
K est compact ssi toutes suites à valeur dans K admet une valeur d'adhérence.

Ensuite deuxième propriété : Dans un espace métrique (ou métrisable) les valeurs d'adhérences d'une suite
sont les limites de ses sous-suite.

Avec ça on démontre que dans un espace métrique :
K compact toutes suites à valeur dans K admet une sous-suite convergente.

Ensuite les propriétés :
i) compact => fermé
ii) fermé et inclus ds un compact => compact

sont vrai dans un espace topologique quelconque.

Dans un espace métrique, on peut montrer de plus que compact => borné.
donc dans un espace métrique on a compact => fermé borné

Maintenant intéressons nous à la réciproque.
Certes dans les evn de dimension fini fermé borné => compact.
Mais est-ce vraiment nécessaire d'être dans un evn ?
Autrement dit existe-il quelque chose qui ne soit pas un espace vectoriel et pour lequel
fermé borné => compact ?
ou a-t-on réellement besoin de toute la structure d'espace vectoriel pour avoir fermé borné => compact ?

En faite ce qui m'interpelle, c'est que pour la réciproque on ait besoin d'avoir des hypothèses aussi fortes.

N.B. : pour certain résultat que j'ai annoncé je crois que l'espace topologique doit être séparé

fermé borné implique :mur: :marteau: compact, c'est faux; point final!!!

[jlb]

Bonjour, jlb

pour le passage auquel tu fais référence, j'utilise le théorème de Bolzano-Weierstrass qui dit que
dans un espace topologique, est compact ssi toute suite à valeur dans admet une valeur d'adhérence.

Pour ce qui est du théorème de Riesz, il me semble que tout espace vectoriel normé de dimension fini
est isomorphe à (à vérifier).

Salut, en fait je ne comprends pas l'argument de prendre une suite dans ton fermé borné de Q qui tendrait vers un irrationnel. En gros, je me demande ce que c'est un fermé borné de Q.

[paquito]

Salut, en fait je ne comprends pas l'argument de prendre une suite dans ton fermé borné de Q qui tendrait vers un irrationnel. En gros, je me demande ce que c'est un fermé borné de Q.

son adhérence est une réunion d'intervalles de R. Donc....

[jlb]

son adhérence est une réunion d'intervalles de R. Donc....

Salut ???? on est dans Q!!! et si c'est un fermé, je vois pas ce que l'adhérence aurait de plus que l'ensemble, non?