Compacité !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Nov 2007, 18:41
par barbu23 » 19 Nov 2007, 18:41
Salut :
Pourquoi si

une application d'un compact

dans un localement compact

, propre est continue ?

est propre signifie que l'image inverse d'un compact par

est compact !
Merci d'avance de votre aide !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Nov 2007, 18:57
par barbu23 » 19 Nov 2007, 18:57
Une deuxième question :
Est ce que vous pouvez m'expliquer un passage ambigue dans ce qui suit :
Il s'agit de montrer que si

est propre alors

est fermé :
Voiçi la démonstration où il y'a le problème :
Supposons que

est propre .
Soit

un fermé de

.
On a
 \subset \overline{f(A)} $)
Montrons que :
} \subset f(A) $)
Soit
} $)
:
Soit

un voisinage compact de

.
Alors :
 \neq \empty $)
Alors
} $)
.
Montrons que
 $)
est fermé.
On a :
 $)
est fermé dans le compact
 $)

 $)
est compact.
Puisque

est contniue , alors
) = f(A) \bigcap K $)
est compact, donc fermé !
D'où :
 $)
Donc
 $)
.
Donc
 $)
est fermé !
Questions :Est ce que vous pouvez m'expliquer comment on est arrivé à
} $)
.
merci d'avance !!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Nov 2007, 20:14
par yos » 19 Nov 2007, 20:14
barbu23 a écrit:comment on est arrivé à
} $)
.
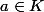
et
})
donc...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Nov 2007, 20:17
par barbu23 » 19 Nov 2007, 20:17
oui mais
} $)
n'est pas inclus dans
 } $)
! non ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Nov 2007, 20:25
par yos » 19 Nov 2007, 20:25
barbu23 a écrit:Pourquoi si

une application d'un compact

dans un localement compact

, propre est continue ?

est propre signifie que l'image inverse d'un compact par

est compact !
Pas d'hypothèse générale sur E? espace métrique? Topologique quelconque? E est-il séparable?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Nov 2007, 20:26
par yos » 19 Nov 2007, 20:26
barbu23 a écrit:oui mais
} $)
n'est pas inclus dans
 } $)
! non ?
Ah oui t'as raison. Je regarderai tout à l'heure.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Nov 2007, 20:30
par barbu23 » 19 Nov 2007, 20:30
yos a écrit:Pas d'hypothèse générale sur E? espace métrique? Topologique quelconque? E est-il séparable?
Non on travaille que dans des espaces topologiques !! et puisque

est compact alors ar définition il est separé !!
Séparable non, je ne sais p pas !! il n'y'a pas separable là !! c'est tout ce qu'il y'a comme données !!
La même chose pour localement compact, par definition il est séparé !!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Nov 2007, 21:34
par yos » 19 Nov 2007, 21:34
Pour
})
, on peut dire ça :
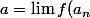, a_n\in A)
. Comme K est un voisinage de a, les
)
sont dans K dés que
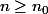
. Donc a est limite d'une suite d'éléments de
)
, ...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Nov 2007, 21:36
par tize » 19 Nov 2007, 21:36
Bonjour,
voici comment je vois les choses :
pour tout voisinage compact

de

, on a
\neq\emptyset)
soit

un voisinage de

que l'on peut supposer compact (car

est localement compact et tout point possède donc une base de voisinages compacts) alors
=\(C\cap K\)\cap f(A)\neq\emptyset)
puisque
\neq\emptyset)
pour tout voisinage compact

de

ce qui est le cas de
)
.
Donc
\)\neq\emptyset)
pour tou voisinage compact

de

, ce qui veut bien dire que
} $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Nov 2007, 22:17
par barbu23 » 19 Nov 2007, 22:17
Merci pour ces reponses là !!
Et pour l'autre question ?
Merci infiniment !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 20 Nov 2007, 09:20
par tize » 20 Nov 2007, 09:20
Bonjour Barbu,
je pense qu'il manque quelque chose pour la première, non ?
si

avec
=1/x)
si
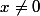
et
=1)
, il me semble que

est propre et que pour la topologie usuelle

est compact et

est localement compact, pourtant

n'est pas continue...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Nov 2007, 09:58
par yos » 20 Nov 2007, 09:58
)
est pas compact non?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 20 Nov 2007, 10:04
par tize » 20 Nov 2007, 10:04
Bonjour Yos,
pourquoi ? j'ai peut être écrit une grosse connerie...mais
=\{0;1\})
, non ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Nov 2007, 10:25
par yos » 20 Nov 2007, 10:25
Oui tu as raison. J'ai mal lu : j'avais pris

comme ensemble de départ (c'est idiot car celui-ci doit être compact).
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 20 Nov 2007, 11:13
par tize » 20 Nov 2007, 11:13
Ah OK, sinon j'ai bien l'impression que notre Barbu à oublié quelque chose...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Nov 2007, 15:57
par tize » 21 Nov 2007, 15:57
UP, alors barbu ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 21 Nov 2007, 17:20
par barbu23 » 21 Nov 2007, 17:20
Salut "tize" , attend je vais voir !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 21 Nov 2007, 17:23
par barbu23 » 21 Nov 2007, 17:23
C'est tous ce que j'ai comme données dans l'énoncé !
-
amine22
- Messages: 4
- Enregistré le: 20 Fév 2007, 20:10
-
 par amine22 » 10 Déc 2007, 16:58
par amine22 » 10 Déc 2007, 16:58
barbu23 a écrit:oui mais
} $)
n'est pas inclus dans
 } $)
! non ?
K est compact donc K est ferme alors adherent(K)=K
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités