Compacité et continuité

[legeniedesalpages]

Bonsoir, je bloque sur cet exo:

Soient et deux espaces métriques, et une application.
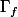
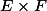
Le graphe de est le sous-espace de défini par:

[CENTER][/CENTER]

On suppose compact.

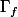
Montrer que si est fermé alors est continue.

Merci pour votre aide.

[Joker62]

Part de la caractérisation séquentielle de la continuïté d'une fonction.

N'oublie pas que dans un compact, toute suite possède au moins une valeur d'adhérence
Et n'oublie pas que dans un fermé, si une suite converge, alors la limite est dans l'espace

[legeniedesalpages]

Part de la caractérisation séquentielle de la continuïté d'une fonction.

N'oublie pas que dans un compact, toute suite possède au moins une valeur d'adhérence
Et n'oublie pas que dans un fermé, si une suite converge, alors la limite est dans l'espace

Salut joker,

je pense bien qu'il faut utiliser la caractérisation séquentielle, mais pourquoi cette valeur serait unique, et serait la limite, c'est cette étape qui me bloque.

[alavacommejetepousse]

bonsoir

c'est le principe du mélange

avec (xn) et (x'n) deux suites de limites toutes deux x admettant chacune une sous suite d'image par f qui converge fabrique s en une troisième

cela prouvera que la limite est indépendante du choix de xn et vaut donc forcément f(x)

[legeniedesalpages]

Je dis n'importe quoi.

Soit . Soit une suite de points de qui tend vers .

La suite telle que pour tout , , est une suite de points de .

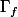
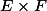
Maintenant il faut montrer que converge dans , et il faudrait que j'utilise l'hypothèse de compacité,

donc comme est compact, il existe une extraction telle que converge. Notons sa limite.

Là j'ai un trou pour arriver à converge.

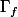
Après comme est fermé on aura bien tend vers .

[alavacommejetepousse]

c'est la suite extraite de u qui converge pas u a priori mais c'est suffisant

[Joker62]

Alors en réduit :

Soit x_n une suite de E qui converge vers x

Soit f(x_n) qui est donc une suite d'élement de F

F compact, on a v_n = f(x_n) admet une sous-suite v_tau(n) qui converge vers un certain y

Soit x_tau(n) la sous-suite associée pour x_n.
x_n converge vers x donc x_tau(n) converge vers x

Ainsi u_n = (x_tau(n) , f(x_tau(n))) converge vers (x,y)
On a bien (x,y) € graphe de f car il est fermé

Reste à montrer que y = f(x)

[legeniedesalpages]

bonsoir

c'est le principe du mélange

avec (xn) et (x'n) deux suites de limites toutes deux x admettant chacune une sous suite d'image par f qui converge fabrique s en une troisième

cela prouvera que la limite est indépendante du choix de xn et vaut donc forcément f(x)

je connaissais pas ce principe, et je ne le comprends pas trop.

Donc je prends et les sous-suites respectives de et telles que leur image par f converge.

J'ne fabrique une troisième:

,


converge vers et son image converge aussi.

mais pourquoi prends celle-ci et pas directement où son image converge (on aurait besoin de qu'une suite au lieu de deux comme ça).

Il y a quelque chose que je ne saisis pas dans ce mélange

[alavacommejetepousse]

le mélange ne s'applique pas ici en fait

u(phi(n)) converge vers un (a,f(a)) donc xphi(n) vers donc a = x


donc toute suite f(x(n)) a une sous suite qui converge vers f(a) ça suffit

[legeniedesalpages]

le mélange ne s'applique pas ici en fait

u(phi(n)) converge vers un (a,f(a)) donc xphi(n) vers donc a = x


donc toute suite f(x(n)) a une sous suite qui converge vers f(a) ça suffit

ah je ne connais pas ce résultat, juste pour qu'on s'accorde:

la caractérisation séquentielle que je possède est

est continue en ssi pour tout suite qui tend vers , tend vers.

Et si j'ai bien compris vous utilisez cette caractérisation:

si pour tout suite qui tend vers , il existe une sous-suite de qui tend vers alors est continue en (ce qui serait donc suffisant).

C'est bien ça?

[alavacommejetepousse]

oui

car si f n 'est pas continue en x il existerait un epsilon et une suite x(n) de limite x telle l f(x(n)- f(x) l > epsilon et ensuite impossible d'extraire une suite de limite f(x)

[legeniedesalpages]

oui

car si f n 'est pas continue en x il existerait un epsilon et une suite x(n) de limite x telle l f(x(n)- f(x) l > epsilon et ensuite impossible d'extraire une suite de limite f(x)

ok c'est plus clair, et je comprends mieux ce que vous me dites, entre autres la version réduite de joker (post #6), donc en reprenant justement son post,

on a (x,y) dans le graphe de f, donc y=f(x).

Merci à vous deux

[Joker62]

Lol !
J'avais même pas vu la subtilité du (x,y) € graphe alors y = f(x)
J'suis pourri comme mec ! :D

Au plaisir ;)
Bonne soirée !
Puis samedi soir, faut pas faire de maths ! :D

[legeniedesalpages]

Lol !
J'avais même pas vu la subtilité du (x,y) graphe alors y = f(x)
J'suis pourri comme mec !

Au plaisir
Bonne soirée !
Puis samedi soir, faut pas faire de maths !

J'avoue

mais bon j'arrive pas à décrocher et puis avec un boulot abrutissant qui fait perdre du temps la semaine j'ai pas trop le choix. :mur: