Comment montrer que un+1/un>2

[RACSO]

Voici l'énoncé (il y a la correction avec ) : http://www.math.jussieu.fr/~polo/1M001/D1-131-corN.pdf

c'est l'exercice 1 que j'ai pas compris, comment as t-on réussi à montrer que un+>2? pourquoi en passant par la lim un+1/un on arrive à montrer que un+1/un>2?
Puis la petite 2 comment arrive t-on à conclure que un est convergente?
Cordialement

[deltab]

Bonsoir.

c'est l'exercice 1 que j'ai pas compris, comment as t-on réussi à montrer que un+>2? pourquoi en passant par la lim un+1/un on arrive à montrer que un+1/un>2?
Puis la petite 2 comment arrive t-on à conclure que un est convergente?
Cordialement

Ce n'est rien d'autre que l'application de la définition de la limite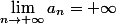 avec A=2 (Quel que soit 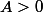, il existe un rang 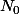tel que ......).

On entend par suite convergente une suite dont la limite est finie. Dans le corrigé il est montré que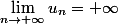 ( donc diverge).