Comment calculer la somme de Riemann suivante ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 23 Mar 2013, 23:38
par HERCOLUBUS » 23 Mar 2013, 23:38
Bonjour à tous !
Je suis un empoté en math qui tente de résoudre le problème suivant:
Soit une fonction
= sqrt{3x+2})
sur [-1,1]. En subdivisant l'intervalle donné en 4 sous-intervalles d'égale largeur et en considérant le point milieu de chacun des sous-intervalles, calculez
la somme de Riemann
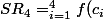 \Delta x_{i})
.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 24 Mar 2013, 00:04
par XENSECP » 24 Mar 2013, 00:04
Donc ça revient à calculer l'intégrale de f(x) entre -1 et 1. Riemann quoi
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 24 Mar 2013, 00:50
par mrif » 24 Mar 2013, 00:50
HERCOLUBUS a écrit:Bonjour à tous !
Je suis un empoté en math qui tente de résoudre le problème suivant:
Soit une fonction
= sqrt{3x+2})
sur [-1,1]. En subdivisant l'intervalle donné en 4 sous-intervalles d'égale largeur et en considérant le point milieu de chacun des sous-intervalles, calculez
la somme de Riemann
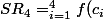 \Delta x_{i})
.
La subdivision demandée est formée des intervalles suivants:
[-1 ; -0.5] , [-0.5 ; 0] , [0 ; 0.5] , [0.5 ; 1];
Les milieux de ces intervalles sont:
c1 = -0.75 c2 = -0.25 c3 = 0.25 c4 = 0.75
Comme les intervalles sont de même longueur les

sont égaux à 0.5.
Donc la somme de Riemann qu'on te demande de calculer est:
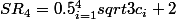
Il reste à remplacer les
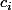
par leurs valeurs et à faire le calcul.
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 25 Mar 2013, 00:16
par HERCOLUBUS » 25 Mar 2013, 00:16
mrif a écrit:La subdivision demandée est formée des intervalles suivants:
[-1 ; -0.5] , [-0.5 ; 0] , [0 ; 0.5] , [0.5 ; 1];
Les milieux de ces intervalles sont:
c1 = -0.75 c2 = -0.25 c3 = 0.25 c4 = 0.75
Comme les intervalles sont de même longueur les

sont égaux à 0.5.
Donc la somme de Riemann qu'on te demande de calculer est:
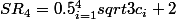
Il reste à remplacer les
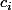
par leurs valeurs et à faire le calcul.
Donc la réponse est:
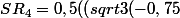+2})+(sqrt{3(-0,25)+2})+(sqrt{3(0,25)+2})+(sqrt{3(0,75)+2})))
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 25 Mar 2013, 00:31
par mrif » 25 Mar 2013, 00:31
HERCOLUBUS a écrit:Donc la réponse est:
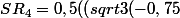+2})+(sqrt{3(-0,25)+2})+(sqrt{3(0,25)+2})+(sqrt{3(0,75)+2})))
C'est ça mais il faut finir les calculs (en utilisant une calculatrice par exemple)
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 25 Mar 2013, 01:05
par HERCOLUBUS » 25 Mar 2013, 01:05
mrif a écrit:C'est ça mais il faut finir les calculs (en utilisant une calculatrice par exemple)
Okay merci !
Ça me donne environ 3,399 comme valeur :zen:
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 25 Mar 2013, 13:21
par Pythales » 25 Mar 2013, 13:21
HERCOLUBUS a écrit:Okay merci !
Ça me donne environ 3,399 comme valeur :zen:
f(x) n'est pas définie en -1 !!!
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 28 Mar 2013, 21:25
par bentaarito » 28 Mar 2013, 21:25
HERCOLUBUS a écrit:Donc la réponse est:
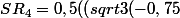+2})+(sqrt{3(-0,25)+2})+(sqrt{3(0,25)+2})+(sqrt{3(0,75)+2})))
ça m'étonne que ta calculatrice n'ait pas ralé :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
sur [-1,1]. En subdivisant l'intervalle donné en 4 sous-intervalles d'égale largeur et en considérant le point milieu de chacun des sous-intervalles, calculez
.
sont égaux à 0.5.
par leurs valeurs et à faire le calcul.