TABLEUR EXCEL : CONCEVOIR UN TABLEAU D'EMPRUNT
ETAPE 5 : LA FINITION
a) LIGNE 21
colonne A : Ecrire TOTAL
colonne C : tapper : =SOMME(C5:C20)
Le résultat apparaît : 310 730.95
colonne E : tapper : =SOMME(E5:E20)
Le résultat apparaît : 17 000.40
colonne F : tapper : =SOMME(F5:F20)
Le résultat apparaît : 293 730.55
b) Faire l'encadrement du tableau.
CONTROLEZ BIEN LES RESULTATS à ce stade.
Ce tableau d'emprunt est terminé.
FIN de l'étape 5 : CONSERVER CE TABLEAU SOUS LE NOM "MATRICE EMPRUNT"
Comment calculer la 1ère mensualité dun prêt à taux fixe à mensualité progressive ?
26 messages
- Page 2 sur 2 - 1, 2
COMMENT COMPLETER CE TABLEAU D'EMPRUNT
a) ce tableau permet de calculer les annuité, des semestrialités, des trimestrialités, des mensualités :
il suffit d'indiquer le TAUX PERIODIQUE EQUIVALENT.
b) si le nombre de lignes du tableau d'emprunt est trop important : supprimer les lignes 5 et suivantes
(mais SURTOUT PAS la PREMIERE LIGNE et la DERNIERE LIGNE)
c) si le nombre de lignes est insuffisant créer de nouvelles lignes à partir de la 5 ème ligne
(mais SURTOUT PAS la PREMIERE LIGNE et la DERNIERE LIGNE)
d) si les ANNUITES sont CONSTANTES : ECRIRE CASE : C4 le chiffre 1
On aura alors un tableau d'emprunts avec annuités constantes
e) les utilisateurs qui savent se servir de EXCEL découvriront par eux-mêmes les
autres possibilités de calculs, à savoir :
* calculer le capital emprunté
* calculer le taux de l'emprunt
* possibilité d'avoir des annuités variables
* possibilité d'avoir des taux d'intérêt variables
* possibilité d'avoir des annuités variables avec des taux variables
* possibilité de calculer la durée : délicat car il faut jouer sur le nombre de lignes
* etc .
a) ce tableau permet de calculer les annuité, des semestrialités, des trimestrialités, des mensualités :
il suffit d'indiquer le TAUX PERIODIQUE EQUIVALENT.
b) si le nombre de lignes du tableau d'emprunt est trop important : supprimer les lignes 5 et suivantes
(mais SURTOUT PAS la PREMIERE LIGNE et la DERNIERE LIGNE)
c) si le nombre de lignes est insuffisant créer de nouvelles lignes à partir de la 5 ème ligne
(mais SURTOUT PAS la PREMIERE LIGNE et la DERNIERE LIGNE)
d) si les ANNUITES sont CONSTANTES : ECRIRE CASE : C4 le chiffre 1
On aura alors un tableau d'emprunts avec annuités constantes
e) les utilisateurs qui savent se servir de EXCEL découvriront par eux-mêmes les
autres possibilités de calculs, à savoir :
* calculer le capital emprunté
* calculer le taux de l'emprunt
* possibilité d'avoir des annuités variables
* possibilité d'avoir des taux d'intérêt variables
* possibilité d'avoir des annuités variables avec des taux variables
* possibilité de calculer la durée : délicat car il faut jouer sur le nombre de lignes
* etc .
COMMENT RESOUDRE UN PROBLEME
On doit résoudre le problème suivant :
Capital emprunté : 360 000,00
Durée : 15 ans
Taux d'intérêt : 0,50 % par an soit 0,00500 pour 1.
Annuité en progression géométrique de raison : 1,005
On demande de calculer le montant de la première annuité.
Pour cela on se place sur la case : C3
On tappe : 25 000,00 et dans la case G19 on a -14 154,64
L'annuité est inférieure
On tappe : 23 000,00 et dans la case G19 on a 18 015,00
L'annuité est supérieure
On tappe : 24 000,00 et dans la case G19 on a 1 930,18
L'annuité est supérieure
On tappe : 24 100,00 et dans la case G19 on a 321,70
L'annuité est supérieure
On tappe : 24 120,00 et dans la case G19 on a zero
L'annuité est de 24 120,00 euros.
Le tableau d'emprunt est terminé
On doit résoudre le problème suivant :
Capital emprunté : 360 000,00
Durée : 15 ans
Taux d'intérêt : 0,50 % par an soit 0,00500 pour 1.
Annuité en progression géométrique de raison : 1,005
On demande de calculer le montant de la première annuité.
Pour cela on se place sur la case : C3
On tappe : 25 000,00 et dans la case G19 on a -14 154,64
L'annuité est inférieure
On tappe : 23 000,00 et dans la case G19 on a 18 015,00
L'annuité est supérieure
On tappe : 24 000,00 et dans la case G19 on a 1 930,18
L'annuité est supérieure
On tappe : 24 100,00 et dans la case G19 on a 321,70
L'annuité est supérieure
On tappe : 24 120,00 et dans la case G19 on a zero
L'annuité est de 24 120,00 euros.
Le tableau d'emprunt est terminé
La formule donnée par BEN314
C = (a/q) * n
avec
C = 360 000,00
q = 1,005
n = 15
Nous donne :
360 000,00 = ( a / 1,005 ) * 15
360 000,00 / 15 = ( a / 1,005 )
24 000,00 = a / 1,005
24 000,00 * 1,005 = a
24 120,00 = a
L'annuité est de 24 120,00 euros
montant identique à celui trouvé dans le tableau d'emprunt.
Merci BEN314, j'étudierai ATTENTIVEMENT votre remarque.
C = (a/q) * n
avec
C = 360 000,00
q = 1,005
n = 15
Nous donne :
360 000,00 = ( a / 1,005 ) * 15
360 000,00 / 15 = ( a / 1,005 )
24 000,00 = a / 1,005
24 000,00 * 1,005 = a
24 120,00 = a
L'annuité est de 24 120,00 euros
montant identique à celui trouvé dans le tableau d'emprunt.
Merci BEN314, j'étudierai ATTENTIVEMENT votre remarque.
Vincent40 a écrit:En cherchant sur le net j'ai trouvé en fait c'est tout simple voici la formule pour la 1ere echeance dans le cas ou le taux d'interets = taux de progression : V0=NA1/(1+P)
avec V0 = Capital initial
N = Durée
P = Taux de progression
A1= 1ère annuité (celle qu'on cherche)
Merci de votre aide
Merci pour votre recherche
Cette formule confirme la démarche de BEN314
Salut,
c'est une question classique en mathématiques financières. Pour y répondre, il faut commencer par le début.
Première étape : si m est l'échéance (mensuelle) constante qui rembourse un crédit d'un montant K sur une durée n (en mois) et si x est le taux de période mensuelle, alors on a nécessairement :^t}=m\times A_n^x=m\times \frac{1-(1+x)^{-n}}{x}) .
.
D'une manière plus générale, si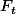 représente l'échéance au rang
représente l'échéance au rang  , on a tout aussi nécessairement :
, on a tout aussi nécessairement : ^t})
Le taux mensuel est quelconque, au sens où il est déduit d'une manière ou d'une autre du taux nominal contractuel du prêt. En général, c'est un taux proportionnel, par exemple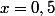 si
si 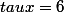 car par définition, un taux est toujours une donnée annuelle, sauf mention contraire.
car par définition, un taux est toujours une donnée annuelle, sauf mention contraire.
Supposons maintenant que le crédit s'amortisse sur la base d'une échéance mensuelle progressant annuellement à un rythme donné, disons . Les 12 premières échéances sont égales à
. Les 12 premières échéances sont égales à 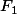 , les 12 suivantes, à
, les 12 suivantes, à 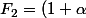\times F_1) , puis
, puis 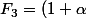^2\times F_1) , usw ...
, usw ...
En reprenant l'équation du début, on a donc, après simplifications :
}{(1+x)^{12}}+ \left(\frac{(1+\alpha)}{(1+x)^{12}}\right)^2+\dots+\left(\frac{(1+\alpha)}{(1+x)^{12}}\right)^{d-1}\right)) avec d = durée en année vérifiant
avec d = durée en année vérifiant 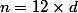 .
.
En définissant tel que
tel que }{(1+x)^{12}}) , on obtient :
, on obtient : 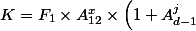) donnant la première échéance d'un prêt à taux fixe et échéance progressive.
donnant la première échéance d'un prêt à taux fixe et échéance progressive.
NB : on peut aller plus loin en supposant qu'en outre, le taux du prêt soit fixé à différents niveaux sur des durées fixées d'avance (grands classiques des formules de crédit à taux et échéances progressives dans les années 80/90).
c'est une question classique en mathématiques financières. Pour y répondre, il faut commencer par le début.
Première étape : si m est l'échéance (mensuelle) constante qui rembourse un crédit d'un montant K sur une durée n (en mois) et si x est le taux de période mensuelle, alors on a nécessairement :
D'une manière plus générale, si
Le taux mensuel est quelconque, au sens où il est déduit d'une manière ou d'une autre du taux nominal contractuel du prêt. En général, c'est un taux proportionnel, par exemple
Supposons maintenant que le crédit s'amortisse sur la base d'une échéance mensuelle progressant annuellement à un rythme donné, disons
En reprenant l'équation du début, on a donc, après simplifications :
En définissant
NB : on peut aller plus loin en supposant qu'en outre, le taux du prêt soit fixé à différents niveaux sur des durées fixées d'avance (grands classiques des formules de crédit à taux et échéances progressives dans les années 80/90).
26 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
