Combinatoire

[yannmaths]

Bonjour, je dois dénombrer le nombre de possibilité d'un certain évènement.
On a 12 éléments à savoir A_1, A_2, A_3, A_4, B_1, B_2, B_3, C_1, C_2, C_3, C_4, C_5.
On doit dénombrer le nombre de permutations tel que il n'y a jamais de A à coté d'un autre A, un B à coté d'un autre B et un C à coté d'un autre C.
Merci pour votre aide et bonne journée.

[GaBuZoMeu]

Bonsoir,

Pas tout à fait évident comme dénombrement.

J'ai commencé par dénombrer les permutations qui commencent par un A et finissent par un C.
J'ai procédé d'une manière qui me semble un peu lourde, mais je n'en vois pas d'autre pour le moment.
On peut noter ab le nombre de passages d'un A à un B, etc.. On écrit alors un système de six équations linéaires entre les six inconnues ab, ac, etc., qui commence avec ab+ac = 5. Le système est de rang 5, on a un degré de liberté limité par le fait que tous ces nombres sont positifs ou nuls.
Et une fois écrites les différentes solutions, on peut dénombrer les mots corrects en A, B, C



et il ne reste plus qu'à multiplier par pour avoir les permutations avec les numéros des A, B et C.

[GaBuZoMeu]

Non, je me suis trompé dans la dernière étape, je compte des mots qui n'existent pas, mon 135 est trop élevé.

On peut tricher et faire un calcul correct en utilisant les outils combinatoires de SageMath :

Code: Tout sélectionner

P=Permutations(5*["A"]+3*["B"]+4*["C"])
M=[p for p in P if all(p[i]!=p[i+1] for i in range(11))]
len(M)

588

Pour les mots qui commencent par A et finissent par C :

Code: Tout sélectionner

N=[p for p in M if (p[0]=="A" and p[-1]=="C")]
len(N)

102

Moins que 135 !

On peut voir la liste des mots qui commencent et finissent par B :

Code: Tout sélectionner

[p for p in M if (p[0]=="B" and p[-1]=="B")]

[['B', 'A', 'B', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'C', 'B'],
['B', 'A', 'B', 'C', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'B'],
['B', 'A', 'C', 'A', 'B', 'A', 'C', 'A', 'C', 'A', 'C', 'B'],
['B', 'A', 'C', 'A', 'B', 'C', 'A', 'C', 'A', 'C', 'A', 'B'],
['B', 'A', 'C', 'A', 'C', 'A', 'B', 'A', 'C', 'A', 'C', 'B'],
['B', 'A', 'C', 'A', 'C', 'A', 'B', 'C', 'A', 'C', 'A', 'B'],
['B', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'B', 'A', 'C', 'B'],
['B', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'B', 'C', 'A', 'B'],
['B', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'C', 'B', 'A', 'B'],
['B', 'A', 'C', 'A', 'C', 'A', 'C', 'B', 'A', 'C', 'A', 'B'],
['B', 'A', 'C', 'A', 'C', 'B', 'A', 'C', 'A', 'C', 'A', 'B'],
['B', 'A', 'C', 'B', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'B'],
['B', 'C', 'A', 'B', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'B'],
['B', 'C', 'A', 'C', 'A', 'B', 'A', 'C', 'A', 'C', 'A', 'B'],
['B', 'C', 'A', 'C', 'A', 'C', 'A', 'B', 'A', 'C', 'A', 'B'],
['B', 'C', 'A', 'C', 'A', 'C', 'A', 'C', 'A', 'B', 'A', 'B']]

Il y en a 16.

Bon, tout ça ne donne pas un bel argument combinatoire pour le dénombrement ...

[tournesol]

Bonjour GaBuZoMeu
Je n'ai pas beaucoup de temps mais je procèderais ainsi:
j'aligne les C :CCCCC
Je place 4 jalons(flags)entre les C: C|C|C|C|C
il reste 3 jalons à places dans 6 places
cela revient à dénombrer le nombre de solutions de l'équation
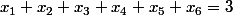sur
Résultat connu ou facile à retrouver
Je place ensuite les A en tenant compte des differents sommants(si un sommant vaut 2, je ne peut placer qu'un seul A de deux façons)
etc.(j'ai pas cherché)
Je multiplie ensuite comme toi.

[GaBuZoMeu]

Oui, le début pas de problème ... mais c'est après ("Je place ensuite les A ... ") que ça se corse sérieusement.

[GaBuZoMeu]

Voila, en réfléchissant mieux j'arrive à une formule pas trop jolie, mais qui marc]he bien :

Code: Tout sélectionner

sum(sum(sum(multinomial(k,l,m)*(-1)**(k+l+m)\
            *binomial(4,k-1)*binomial(2,l-1)*binomial(3,m-1)\
            for m in range(1,5)) for l in range(1,4)) for k in range(1,6))

588

Outils :
- formule du crible de Poincaré en considérant les ensembles de mots avec 5 A, 3 B et 4 C qui ont la lettre X (dans {A,B,C}) à la fois en position i et i+1 (avec i compris entre 1 et 11).
- à chaque élément de , associer le mot réduit de longueur où on fusionne les lettres en position et pour chaque .