Combinaison linéaire de racines complexes

[Ben34]

Bonjour !

Je suis en train de remettre le nez dans les équations différentielles, et je bloque dans le cas de la résolution d'équations d'ordre 2 du type C1y''+ C2y' + C3y = 0 à discriminant négatif.

J'ai bien saisi que les deux solutions de l'équation caractéristique sont des racines complexes de la forme a+ib et a-ib, ce qui donne comme solutions de l'équation :
y1=e(a)(cos(bx)+isin(bx)) et
y2=e(a)(cos(bx)-isin(bx))

Cependant, je vois ensuite qu'on fait deux combinaisons linéaires telles que
(y1+y2)/2=e(a)cos(bx) et (y1-y2)i/2=e(a)sin(bx)

d'où la solution générale y= e(a)(cos(bx)+sin(bx)).

Ma question est : d'où vient cette combinaison linéaire ? Pourquoi la fait on ? (ça fait deux questions finalement)

Merci d'avance !

[Mimosa]

Bonjour

Tu n'as pas précisé si les coefficients sont réels ou pas forcément. S'ils ne sont pas réels, la transformation proposée n'a aucun intérêt. En revanche, s'ils sont réels et si on cherche des solutions réelles, c'est la meilleure méthode pour les trouver toutes. On applique les formules d'Euler et on a gagné!
C'est ce que tu voulais savoir?

[Al-Kashi]

Bonsoir Ben314,
La combinaison linéaire est utilisée pour obtenir une solution réelle. Par exemple, en physique, y(t) peut représenter l'intensité du courant électrique, la charge d'un condensateur, la position d'un oscillateur amorti .... qui sont des grandeurs réelles...

[Ben34]

Bonjour, Mimosa, Bonjour Al-Kashi (big up pour le pseudo)

Ok !! J'avais complètement oublié les formules d'Euler !! Et je me suis trompé en appliquant l'appliquant au sinus : le facteur i est censé être au dénominateur ! Si j'ai bien compris, l'astuce permet de "faire passer à la trappe" la composante complexe de chaque solution ?


Je ne comprends par contre pas pourquoi :

Si y1=(y1+y2)/2 alors e(a)(cos(bx)+isin(bx))=cos(bx)

Je comprends qu'on ne puisse pas représenter physiquement un signal complexe. Mais j'ai du mal avec un raisonnement du type "ouai mais bon.. il existe ce signal, donc on fait la formule d'Euler et voila ça annule la composante complexe". Ce n'est pas très clair pour moi encore ! Y'a-t-il quelque chose que je loupe ?

Merci en tout cas pour vos réponses, elles m'aident beaucoup !

[Mimosa]

Tout simplement si tu calcules, tu trouves et .
La première est réelle et la deuxième imaginaire pure!

[Ben314]

Salut,
Une remarque vu que c'est la 3em fois sur ce post que je vois la me erreur (qu'au départ j'ai pris pour une faute de frappe....) : si une des racines complexe du polynôme caractéristique est alors ça donne comme solution pour l'équation

Et pas qui en plus n'a pas franchement de sens vu que l'ensemble des solutions, c'est un espace vectoriel donc pour trouver une base on est pas à un facteur multiplicatif constant prés (=> le exp(a) sans le x n'aurait aucune utilité vu que ça serait un facteur multiplicatif constant.)

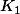Sinon, le passage par les complexe, ben (comme quasi toujours), il est lié au fait que les calculs sont bien plus simple dans C que dans R et là, par exemple, les solutions complexes de l'équation différentielle, c'est tout bètement les fonctions avec et 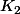deux constantes complexes quelconques (et où sont les solutions complexes conjuguées du polynôme caractéristique).

Et si on cherche les solutions réelles de l'équation, ben le truc évident, c'est que c'est pas en prenant pour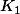 et 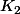des réels que ça marche vu que les fonctions ne sont pas des fonctions réelles.
Donc il faut chercher quelles sont les fonctions réelles de la forme (où ) qui sont réelles.
Et un petit calcul (qu'il faut évidement savoir faire) montre que ce sont celles de la forme avec et 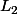deux constantes réelles.
Et c'est même on ne peut plus utile de savoir qu'elles peuvent aussi (toutes) s'écrire sous la forme avec et deux constantes réelles.

[Ben34]

Je crois que j'avais une fausse définition de la combinaison linéaire : je comprends en fait pourquoi on fait la combinaison linéaire de chaque solution pour avoir la solution générale. Maintenant, j'en suis à essayer de comprendre ce que viennent faire les formules d'Euler.

Tout simplement si tu calcules, tu trouves et .
La première est réelle et la deuxième imaginaire pure!

Ok mais... pourquoi on fait ça ? Je veux dire, oui, je constate que du coup, si on applique les formules d'Euler jusqu'au bout on n'a plus les composantes complexes. Sauf que je ne pense pas qu'on soit sur une opération "sortie du chapeau". Ma question c'est : pourquoi on arrive à une solution réelle de cette façon ? En quoi c'est mathématiquement viable ?

Bien vu, c'est une erreur d'inattention, mes excuses !

Donc il faut chercher quelles sont les fonctions réelles de la forme (où ) qui sont réelles.
Et un petit calcul (qu'il faut évidement savoir faire) montre que ce sont celles de la forme avec et deux constantes réelles.

C'est justement ce petit calcul (qu'il faut évidement savoir faire) qui me pose problème j'ai l'impression.