Voila une facon de rédiger afec les "sigma" :
<br />\Big(\bigsum_{|m|\le K}d_me^{im\omega_o}\Big))
Note qu'ici, il est malin de prendre deux lettres différentes dés le début.
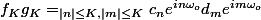
Ici, on a développé : on a donc tout les produits imaginable d'un terme de la première somme par un terme de la deuxième somme.
On peut évidement écrire cela avec un "double sigma" mais on peut l'écrire avec un seul : cela vient simplement du fait que l'addition est commutative et associative : on peut faire des additions dans l'ordre que l'on veut.
\omega_o})
Là, il n'y a rien à dire...
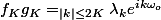
Ici, on regrouppe tout les termes ayant le même
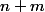
. Si on écrivait les somme avec des points de suspention, cela reviendrait à mettre en facteur les termes ayant le même
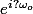
.
On utilise aussi le fait qu'au maximum/minimum,
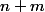
vaut
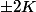
.
Reste à expliciter qui est
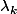
dans la formule :
c'est ce que l'on a mis en facteur c'est à dire la somme de tout les
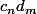
tels que
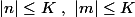 ET
ET 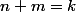
:
Pour tout
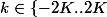
on a
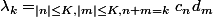
Enfin,on peut écrire cette somme plus simplement en constatant que les trois conditions
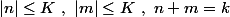
peuvent s'écrire
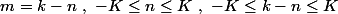
soit encore
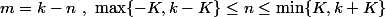
On peut donc écrire :
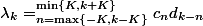
Ou encore
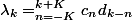
pour
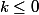
et
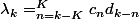
pour
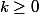
Enfin la dernière solution est d'écrire
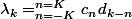 en précisant que
en précisant que lorsque
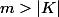
on considère que
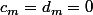
(mais il faut absolument écrire cette précision...)
