Classes de conjugaison de S_n

[pringuez]

Bonjour,

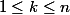
Je cherche à montrer que deux permutations de sont conjuguées si et seulement si pour tout , le même nombre de cycles apparaît dans leurs décompositions respectives en produit de cycles à supports disjoints.

Je sais déjà que :

1) Le conjugué d'un cycle est un cycle :
Plus précisément, ;

2) Deux cycles sont toujours conjugués dans :
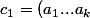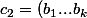Si et , on définit par pour et pour . On a alors .

J'ai réussi à montrer que si deux permutations étaient conjuguées, alors, elles admettaient le même nombre de cycles dans leurs décompositions respectives, pour tout .
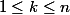
Mais je n'arrive pas à montrer la réciproque...

[GaBuZoMeu]

C'est pourtant juste une généralisation de ce qui se passe en 2), quand on a d'un côté

et de l'autre
.

[pringuez]

Je me doute bien que c'est une généralisation du point 2) (c'est pour cela que je détaille comme je l'ai démontré), mais je n'arrive pas à écrire la permutation par laquelle il faut conjuguer...

[GaBuZoMeu]

????


Au fait, je m'aperçois que tu fais une erreur dans le cas d'un seul cycle : on ne prend sûrement pas quand est en dehors du support du premier cycle : on risquerait de se trouver dans le support du second !

[pringuez]

Intuitivement, j'ai envie d'écrire , mais je n'arrive pas à justifier que ça fonctionne.

[GaBuZoMeu]

Ce n'est pas différent du cas d'un seul cycle (à condition de corriger l'erreur que j'ai signalée).

[pringuez]

Du coup on la construit comment alors la permutation dans le cas d'un seul cycle ?
On peut juste dire que puis que l'on complète le reste "comme on veut" du moment que c'est une bijection de vers ?

[pringuez]

Bon, je pense avoir compris le truc :

En reprenant les notations introduites dans les messages précédents :

a) Pour le cas d'un seul cycle : on impose juste que et on complète le reste "n'importe comment" du moment que soit bien une bijection.

b) Pour le cas général, on impose juste que et on complète le reste "n'importe comment" du moment que soit bien une bijection.
On a alors
Or, , pour tout .
Donc, .

C'est correct ?

[GaBuZoMeu]

Ben oui.
On peut prendre comme restriction de au complémentaire de la réunion des supports de la première collection de cycles disjoints n'importe quelle bijection sur le complémentaire de la réunion des supports de la deuxième.