Bonjour,
Pouriez vous m'aider à comprendre l'énoncé suivant ? :
Les classes de conjugaison d'un groupe symétrique sont composées de produits de cycles à supports disjoints de même structure. Ceci signifie que le nombre de cycles de même longueur est le même pour chaque élément d'une classe de conjugaison.
Je comprend la première phrase à priori. C'est la seconde qui me pose problème. Quelqu'un pour me l'expliquer ?
Merci d'avance !
Classes conjugaison groupe symetriques.
3 messages
- Page 1 sur 1
Re: Classes conjugaison groupe symetriques.
Salut,
Effectivement, c'est chaud de chez chaud comme façon de dire les trucs : j'ai relu 4 fois la phrases et les 3 premières fois je me suis dit que c'était sans queue ni tête et à la 4em je pense avoir compris (et il me semble que c'est du Français correct, mais... pas facile à comprendre....).
Donc je vais réexprimer le truc tel que ça me vient à l'esprit :
Si tu prend une permutation qui, lorsqu'on la décompose comme cycles à supports disjoints, est composée par exemple d'un 2 cycle, de deux 3-cycles et d'un 5-cycle (qui commutent bien sûr entre eux vu qu'ils sont à support disjoint) alors toute permutation
qui, lorsqu'on la décompose comme cycles à supports disjoints, est composée par exemple d'un 2 cycle, de deux 3-cycles et d'un 5-cycle (qui commutent bien sûr entre eux vu qu'ils sont à support disjoint) alors toute permutation 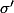 qui est dans la même classe de conjugaison que
qui est dans la même classe de conjugaison que  est elle aussi composée d'un 2 cycle, de deux 3-cycles et d'un 5-cycle.
est elle aussi composée d'un 2 cycle, de deux 3-cycles et d'un 5-cycle.
Bref, tout ça c'est pour essayer d'exprimer dans le cas général ce qui est super simple à exprimer sur un cas particulier : si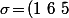(2\ 4)(3\ 7)) et qu'on conjugue
et qu'on conjugue  avec une autre permutation
avec une autre permutation  quelconque on obtient
quelconque on obtient 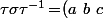(d\ e)(f\ g)) où
où  sont en fait les images respectives de
sont en fait les images respectives de  par
par  .
.
On peut donc dire que et
et  sont "de même structure" (phrase 1) ou bien que "le nombre de cycles de même longueur" de
sont "de même structure" (phrase 1) ou bien que "le nombre de cycles de même longueur" de  et
et  est le même (phrase 2).
est le même (phrase 2).
Effectivement, c'est chaud de chez chaud comme façon de dire les trucs : j'ai relu 4 fois la phrases et les 3 premières fois je me suis dit que c'était sans queue ni tête et à la 4em je pense avoir compris (et il me semble que c'est du Français correct, mais... pas facile à comprendre....).
Donc je vais réexprimer le truc tel que ça me vient à l'esprit :
Si tu prend une permutation
Bref, tout ça c'est pour essayer d'exprimer dans le cas général ce qui est super simple à exprimer sur un cas particulier : si
On peut donc dire que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Classes conjugaison groupe symetriques.
Ok ok, merci beaucoup Ben314 !
Effectivement on comprend mieux ainsi !
Effectivement on comprend mieux ainsi !
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
