Classement ordonné d'une suite

[jacques26]

Soit une suite dans ]0;1].Sous quelles conditions peut-on en faire une suite strictement décroissante ? (En faisant intervenir éventuellement limsup,liminf,sup,inf qui existent d'aprés Bolzano-Weierstrass).
Merci d'avance.

[serge75]

Joli exo......
Je me lance, en n'étant pas 100% sûr de moi.
Tout d'abord, une précision sur l'énoncé : qu'entends-tu par 'en faire' une suite décroissante ? Je propose ma traduction : j'entends par là trouver une permutation des termes de la suite telle qu'on obtienne une suite déroissante. En termes plus précis, trouver une bijection f de N dans N telle que la suite soit décroissante.

Ta suite est bornée, donc a de toutes façons une valeur d'adhérence.

1 - Si ta suite avait deux valeurs d'adhérences distinctes, L et L'. Il exsite alors deux voisinages V et V' de L et L' respectivement tels que (si LN tel que v_p soit dans V' et donc v_p>v_n).
Première conclusion : si (u_n) permet de fabriquer une suite décroissante, alors (u_n) a une seule valeur d'adhérence.

2 - Toute suite bornée ayant une seule valeur d'adhérence converge. En effet si tel n'était pas le cas, il existerait un epsilon>0 et une infinité de n tels que . On en déduit alors une suite extraite (v_n) telle que pour tout n on ait : . (v_n) est bornée et a donc une valeur d'adhérence bien évidemment distincte de L, donc on a trouvé une autre valeur d'adhérence à (u_n) : absurde.
Conclusion : si ta suite convient, alors elle converge.

3 - On suppose donc que (u_n) convient et converge. On appelle toujours (v_n) la suite fabriquée à partir de (u_n), décroissante. Montrons que (v_n) converge vers la même limite notée L.
Epsilon>0 étant fixé, il y a au plus un nombre fini de n tels que u_n soit éloigné de L d'une distance >epsilon. De la bijectivité de f, il en est de même pour (v_n) et en prenant N plus grand que le dernier n tel que |v_n-L|>epsilon, on a pour n>N |v_n-L|=L, et de même pour les u_n.
Conclusion : on a la condition nécessaire suivante :
Si (u_n) convient, elle est convergente et tous les u_n sont plus grands que sa limite.

4 - reste à regarder la réciproque... J'ai la flemme dans l'immédiat, mais promis je la donnerai dans la soirée si personne ne l'a fait d'ici là.

Serge (en espérant e pas avoir dit trop de bêtises).

[bauzau]

la suite est borné donc (bolzano-w) il existe au moins une valeur d'adhérence.

je pense qu'il y a 2 conditions:

(1) il faut que la val d'adh soit unique

notons x la val d'adh, alors

(2) il faut que quelque soit n, U(n)>=x

[serge75]

Comme personne n'a été inspiré, je me colle à la réciproque.
On considère donc une suite (u_n) de ]0,1], convergente vers L, et telle que pour tout n on ait u_n>=L.

1 - J'appelle l'ensemble de tous les et je vais montrer que a un plus grand élément.
Soit x le sup de qui lui existe. Si x n'était pas atteint, il existerait une suite d'éléments de qui convergerait vers x. Comme x n'est pas dans il n'est pas restrictif de supposer que les sont tous distincts, et partant de là, en 'remettant les indices dans l'ordre' (je passe les détails techniques) on obtient une suite extraite de qui converge vers x. Finalement sachant la convergence de j'en déduis que . Par suite tous les sont égaux à L ce qui contredit que x n'est pas dans .

2 - Je pose alors pour f(0) l'un des n tel que .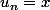

3 - Je prends alors l'ensemble de tous les pour n décrivant N-{f(0)}
De même a un plus grand élément x1 et je pose f(1) l'un des n dans tels que .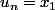
De la définition de j'ai alors et .

4 - On itère le procédé. On obtient ainsi une fonction f injective telles que soit décroissante.

5 - Reste à justifier que f est surjective. Supposons qu'il existe un n qui n'ait pas d'antécédent par f.

J'arrête tout, je me rends compte que ma condition nécessaire n'est pas suffisante : prendre et
On n'est néanmoins pas trop loin du but.... j'y reviens ultérieurement sauf si quelqu'un achève cet exo d'ici là.
Serge