Un circuit délicat à négocier

[Pythales]

Bonjour à tous
Je bute sur cette question, cinquième et dernière d'un problème :
En intégrant le long d'un contour convenablement choisi, trouver la valeur des intégrales et
J'ai pris comme contour un demi cercle de rayon infini de diamètre l'axe des complété d'une coupure verticale partant de , entoutant le point et revenant à
Dans ce contour, la fonction est uniforme et a les pôles et
J'utilise l'égalité
Mon problème est que dans ce circuit, je retrouve bien la 1ère intégrale, mais je n'arrive pas à faire apparaître la 2ème car l'aller-retour le long de la coupure verticale annule son expression (j'espère être clair).
Peut-être faut-il choisir un autre contour. A titre d'information, la valeur de la 1ère intégrale (calculé dans les questions précédentes) vaut
Merci de vos suggestions.

[Ben314]

Salut,
Comme toujours en analyse complexe, il faut déjà préciser quelle determination tu prend pour la fonction et pour la fonction :
Si tu prend la détermination dite principale du , c'est à dire celle définie sur puis que tu prend alors ta fonction est définie sur privé de la demi droite , ainsi que de la demi droite , (fait un dessin).

Conclusion : le contour dont tu parle n'est pas contenu dans le domaine de définition de ta fonction Arctg (car il coupe la demi droite , ) donc on ne risque pas d'intégrer sur ce contour !!!

A mon avis, tu ferais mieux de prendre une détermination de définie sur privé des (fait un dessin) et un parcours adapté au domaine de définition de cette détermination...

[Pythales]

J'avoue que je ne comprends pas très bien ton argumentation.
Pour moi, la fonction n'est indéfinie qu'au point qui s'appelle d'ailleurs point critique logarithmique. La coupure que je fais évite que, dans le domaine, on puisse tourner autour du point qui est le seul point critique logarithmique à prendre en compte, puisque je ne considère que le demi plan supérieur.
Par ailleurs, si je veux pouvoir calculer les 2 intégrales, il faut bien que le contour comprenne un chemin allant de - à + , ainsi qu'un chemin allant de à , même si ce dernier est sur l'axe
Peux-tu préciser ta pensée ?

[Ben314]

Ben, ma pensée, c'est déjà qu'il est impossible de définir une fonction continue Ln sur C*(ou, si tu préfère, une fonction z->Ln(z-a) continue sur C-{a}).
La preuve la plus simple que la fonction z->1/z n'admet pas de primitive sur C* est le fait que, si l'on l'intégre sur un laçet qui fait le tour de 0, on n'obtient pas 0...
Pour définir une fonction logarithme, il faut avoir comme ensemble de départ un ouvert simplement connexe contenu dans C*, par exemple C* privé d'une demi droite d'origine 0.
La demi-droite fréquement enlevée est celle des réels négatifs et, dans ce cas, on parle de "détermination principale" du logarithme.

Pour réviser un peu, tu peut aller regarder sur wikipédia

[Pythales]

Je crois avoir compris ce que tu veux dire : il faut une coupure pour éviter que, tout en restant dans le domaine, on puisse tourner autour du point critique.
Mais dans le contour que je propose, c'est bien le cas, puisque la coupure allant de à empêche de tourner autour de .
Lorsque je parcours le circuit, je pars de avec la détermination pour puis je vais :
- de à + sor l'axe ce qui me donne la moitié de ma 1ère intégrale
- sur la demi circonférence de centre dont le rayon tend vers le long de laquelle l'intégrale tend vers
- de - a , le long des négatifs, ce qui donne encore (à quelque chose près) la 1ère intégrale
- de à ce qui donne (toujours à quelque chose près) la 2ème intégrale
- autour d'un petit cercle de centre et dont le rayon tend vers le long duquel l'intégrale tend vers
- de à pour revenir au point de départ.
L'ennui est que ce dernier parcours annule celui qui va de à , et c'est là justement tout mon problème.
J'espère avoir été plus clair. Un petit dessin eut peut-être été plus explicite ...

[Ben314]

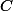
Effectivement, on peut definir une détermination de l'arctangente (en temps que primitive de 1/(1+z²) ) sur privé de la demi droite avec (en fait on peut même n'enlever que le segment [-i,i] mais, vu le parcours que tu veut prendre, cela ne set à rien...)
MAIS,
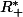
1) Il faut faire attention au fait que, dans ce cas, ta détermination n'est pas définie en z=0 et elle ne peut pas coïncider avec l'arctangente réelle usuelle à la fois sur et sur : il y aura un 'décalage' d'une constante au moins d'un des deux cotés.
2) Cette détermination de l'arctangente ne peut pas être définie par

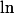
Une façon de définir cette détermination particulière est de poser où est la détermination principale du log (i.e. celle définie sur et valant 0 au point z=1).
Dans ce cas, si on note (sans majuscule) la fonction arctangente usuelle sur , on a :
- Pour tout ,
- Pour tout ,

Edit : si dans ton précedent message le "à quelque chose prés" correspond au "décalage" entre les fonctions Arctg et arctg sur les réels strictement négatifs, c'est O.K.
Par contre, le deux intégrales le long du segment [0,i] (une fois légèrement à droite du segment et de haut en bas puis l'autre fois légèrement à gauche et de bas en haut) ne s'annulent pas mutuellement car la fonction Arctan ne prend pas la même valeur légèrement à droite du segment que celle qu'elle prend légèrement à gauche (sinon, on n'aurait pas été obligé d'enlever le segment de son domaine de définition !!!)
Attention aussi à justifier soigneusement le fait que l'intégralle le long du (presque) cercle entourant le point tend bien vers 0 lorsque le rayon du cercle tend vers 0.

[Pythales]

Pour être précis, il est clair que les 2 intégrales à gauche et à droite du segment n'ont pas la même valeur, mais lorsqu'on tourne autour de , est multiplié par , ce que le transforme en somme. On retrouve bien d'un côté et de l'autre, qui s'annulent, et c'est là encore une fois le problème. Ce qui ne s'annule pas ce sont des sommes (ou des différences) d'exponentielles.
J'espère encore une fois être assez clair...

[Ben314]

En constatant que (à l'aide du changement de variable x=1/y) on voit que ce qui correspond (à quelques constantes prés...) à l'arctangente sur l'axe imaginaire "positif".
Je pense donc que l'on peut obtenir les deux intégrales en prenant comme parcours R+ puis un trés grand quart de cercle puis iR+.
Mais ce n'est pas totalement direct...

[Pythales]

Bien vu.
Et en plus on n'a qu'un pôle à prendre en compte.
Je vais exploiter ça.

[Pythales]

Ca marche, et on trouve
Merci.

[Ben314]

Impec...
Le seul truc qui me semble un peu bizare, c'est qu'en général, dans ce genre d'exo, quand on demande "en déduire la valeur de l'intégrale réelle...", c'est une déduction "directe" alors que là, c'est un peu plus "finassous".
Il y a donc peut-être une autre façon de faire...