Changement de variable, double intégrale, cylindrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
masque gazé
- Membre Naturel
- Messages: 45
- Enregistré le: 11 Déc 2014, 15:12
-
 par masque gazé » 08 Jan 2015, 15:59
par masque gazé » 08 Jan 2015, 15:59
Salut.
J'aurais besoin d'aide en ce qui concerne les variations de r dans cette exercice:
: }<br />\\<br />\text{Prenons pour exemple: }I=\displaystyle\int_0^\infty e^{-x^2}dx\\<br />\\<br />\textbf{Il faut d'abord elever }I\textbf{ au carre: }\\<br />I^2=\displaystyle\int_0^\infty e^{-x^2}dx\times\int_0^\infty e^{-y^2}dy\\<br />\\<br />\text{Grace au theoreme de Fubini:}\\<br />\begin{array}{l c r}<br />I^2=\displaystyle\int_{\mathbb{R}^+\times \mathbb{R}^+} e^{-x^2}.e^{-y^2}d\big(\lambda(x)\otimes \lambda (y)\big)\\<br />\\<br />\hspace{0.45cm}= \displaystyle\int_0^{\infty}\int_0^{\infty} e^{-(x^2+y^2)}dx.dy<br />\end{array}\\<br />\\<br />\text{Maintenant changeons pour la base polaire:}\\<br />\varphi:\left\{<br />\begin{array}{l c r}<br />x=r\cos(\theta)\\<br />y=r\sin(\theta)<br />\end{array}<br />\right.\\<br />\\<br />\varphi(r,\theta)\text{ est bijective}\\<br />J_\varphi(r,\theta)=r\neq 0\\<br />\Longleftrightarrow\\<br />\varphi(r,\theta)\text{ est un homeomorphisme et donc}\\<br />\text{on peut utiliser: }\boxed{\displaystyle\int_{V}f(x)dx=\int_{U}f\circ\varphi(u)|J_\varphi(u)|du}\\<br />\\<br />\textbf{Nouveau domaine de définition}\\<br />\textbf{pour }\theta\textbf{ et }r:\\<br />\\<br />\text{Pour balayer l'aire sous }e^{-x^2}\text{ sur }[0,+\infty[\\<br />\theta\text{ doit varier sur } [0,\frac{\pi}{2}] \text{ et }r\text{ sur }[0,+\infty[\\<br />\\<br />\textbf{Valeur de }d\theta\textbf{ et }dr:\\<br />\boxed{\begin{matrix}<br />\text{On utilise ici }\varphi\text{, mais on aurait pu utiliser }\varphi^{-1}\\<br />\text{Si on utilise }\varphi^{-1} \Rightarrow dx.dy=|J_{\varphi^{-1}}|.dr.d\theta\\<br />\text{Si on utilise }\varphi \Rightarrow dx.dy=|J_{\varphi}|.dr.d\theta\\<br />\\<br />PS: J_{\varphi^{-1}}=\frac{1}{J_{\varphi}}\end{matrix}}\\<br />\\<br />\text{Ici }dx.dy=|J_{\varphi}|.dr.d\theta=r.dr.d\theta\\<br />\\<br />\begin{array}{l c r}<br />\text{Donc }I^2= \displaystyle\int_0^{\frac{\pi}{2}}\int_0^\infty r.e^{-\bigg(r^2\big(\cos(\theta)^2+\sin(\theta)^2\big) \bigg) }dr.d\theta\\<br />\hspace{1.35cm}=\displaystyle\int_0^{\frac{\pi}{2}}\displaystyle\int_0^\infty r.e^{-r^2}dr.d\theta\\<br />\hspace{1.35cm}=\big[\theta\big]_0^\frac{\pi}{2}\big[\frac{-e^{-r^2}}{2}\big]_0^\infty\\<br />\hspace{1.35cm}=\frac{\pi}{4}<br />\end{array}<br />\\<br />\Longrightarrow I=\sqrt{\frac{\pi}{4}}=\frac{\sqrt{\pi}}{2}<br />\end{matrix}})
Ma question est: Pourquoi r doit varier dans

et non pas dans un interval du genre
[)
?
Merci pour vos réponses


-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 08 Jan 2015, 16:20
par capitaine nuggets » 08 Jan 2015, 16:20
Salut !
x et y doivent décrire le quart de plan
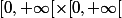
donc de manière polaire,

doit varier dans
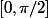
et
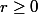
.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 08 Jan 2015, 17:07
par Pythales » 08 Jan 2015, 17:07
masque gazé a écrit:Salut.
J'aurais besoin d'aide en ce qui concerne les variations de r dans cette exercice:
: }<br />\\<br />\text{Prenons pour exemple: }I=\displaystyle\int_0^\infty e^{-x^2}dx\\<br />\\<br />\textbf{Il faut d'abord elever }I\textbf{ au carre: }\\<br />I^2=\displaystyle\int_0^\infty e^{-x^2}dx\times\int_0^\infty e^{-y^2}dy\\<br />\\<br />\text{Grace au theoreme de Fubini:}\\<br />\begin{array}{l c r}<br />I^2=\displaystyle\int_{\mathbb{R}^+\times \mathbb{R}^+} e^{-x^2}.e^{-y^2}d\big(\lambda(x)\otimes \lambda (y)\big)\\<br />\\<br />\hspace{0.45cm}= \displaystyle\int_0^{\infty}\int_0^{\infty} e^{-(x^2+y^2)}dx.dy<br />\end{array}\\<br />\\<br />\text{Maintenant changeons pour la base polaire:}\\<br />\varphi:\left\{<br />\begin{array}{l c r}<br />x=r\cos(\theta)\\<br />y=r\sin(\theta)<br />\end{array}<br />\right.\\<br />\\<br />\varphi(r,\theta)\text{ est bijective}\\<br />J_\varphi(r,\theta)=r\neq 0\\<br />\Longleftrightarrow\\<br />\varphi(r,\theta)\text{ est un homeomorphisme et donc}\\<br />\text{on peut utiliser: }\boxed{\displaystyle\int_{V}f(x)dx=\int_{U}f\circ\varphi(u)|J_\varphi(u)|du}\\<br />\\<br />\textbf{Nouveau domaine de définition}\\<br />\textbf{pour }\theta\textbf{ et }r:\\<br />\\<br />\text{Pour balayer l'aire sous }e^{-x^2}\text{ sur }[0,+\infty[\\<br />\theta\text{ doit varier sur } [0,\frac{\pi}{2}] \text{ et }r\text{ sur }[0,+\infty[\\<br />\\<br />\textbf{Valeur de }d\theta\textbf{ et }dr:\\<br />\boxed{\begin{matrix}<br />\text{On utilise ici }\varphi\text{, mais on aurait pu utiliser }\varphi^{-1}\\<br />\text{Si on utilise }\varphi^{-1} \Rightarrow dx.dy=|J_{\varphi^{-1}}|.dr.d\theta\\<br />\text{Si on utilise }\varphi \Rightarrow dx.dy=|J_{\varphi}|.dr.d\theta\\<br />\\<br />PS: J_{\varphi^{-1}}=\frac{1}{J_{\varphi}}\end{matrix}}\\<br />\\<br />\text{Ici }dx.dy=|J_{\varphi}|.dr.d\theta=r.dr.d\theta\\<br />\\<br />\begin{array}{l c r}<br />\text{Donc }I^2= \displaystyle\int_0^{\frac{\pi}{2}}\int_0^\infty r.e^{-\bigg(r^2\big(\cos(\theta)^2+\sin(\theta)^2\big) \bigg) }dr.d\theta\\<br />\hspace{1.35cm}=\displaystyle\int_0^{\frac{\pi}{2}}\displaystyle\int_0^\infty r.e^{-r^2}dr.d\theta\\<br />\hspace{1.35cm}=\big[\theta\big]_0^\frac{\pi}{2}\big[\frac{-e^{-r^2}}{2}\big]_0^\infty\\<br />\hspace{1.35cm}=\frac{\pi}{4}<br />\end{array}<br />\\<br />\Longrightarrow I=\sqrt{\frac{\pi}{4}}=\frac{\sqrt{\pi}}{2}<br />\end{matrix}})
Ma question est: Pourquoi r doit varier dans

et non pas dans un interval du genre
[)
?
Merci pour vos réponses

Quelle que soit la valeur de

,

varie de

à

-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 08 Jan 2015, 18:26
par paquito » 08 Jan 2015, 18:26
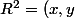 x\in R, y\in R)
ou
, r\geq 0 et -\pi <\theta \leq \pi)
.
-
masque gazé
- Membre Naturel
- Messages: 45
- Enregistré le: 11 Déc 2014, 15:12
-
 par masque gazé » 08 Jan 2015, 18:53
par masque gazé » 08 Jan 2015, 18:53
Merci, en effet je pensais que r devais varier de sorte à ce que l'on recouvre QUE la surface sous la courbe.
Maintenant c'est clair, merci ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités