Champ scalaire polynômial en ses deux variables

[Nightmare]

Salut à tous !

On m'a posé le problème suivant il y a longtemps, je n'avais pas trouvé à l'époque, je viens de le ressortir du tiroir et... je n'ai toujours pas trouvé :lol3:

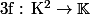
On prend un champ scalaire : qui est polynômial en ses deux variables.

Si K est fini, f est un polynôme (évident, même sans les hypothèses :lol3: )

Si K=R ou C, est-ce toujours vrai? Si K=Q ?

J'ai une petite idée pour R, aucune pour Q, ça me semble bien plus compliqué !

A vos stylos si ça vous intéresse ! J'y réfléchis aussi.

Edit : Je précise que l'hypothèse est que les applications et sont des polynômes respectivement en x quel que soit y pour la première et en y quel que soit x pour la seconde. Des polynômes à coef dans K évidemment.

[Doraki]

Ca veut dire quoi, polynomial ? ses restrictions à des lignes horizontales ou verticales sont des polynômes ?

[Nightmare]

C'est ça, les applications x->f(x,y) et y-> f(x,y) sont des polynômes.

[wserdx]

Qu'est-ce que tu entends par f polynomial? univarié? si oui sur quel corps?
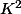
Pour un corps fini, si on considère comme une extension de degré 2 de , les fonctions coordonnées sont des polynômes
puisque de la forme où .

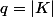
[Nightmare]

wserdx -> Cf mon post précédent.

Pour le cas fini, il me semble que tout champ scalaire sur un corps fini est un polynôme.

[wserdx]

Euh, je n'ai pas compris ta question.
Je vois bien quelle est l'hypothèse, mais qu'est-ce qu'il faut montrer alors?

[Nightmare]

Il faut montrer que f est un polynôme (en les deux indéterminées x et y).

Autrement dit, montrer que si x->f(x,y) est dans K[x] quel que soit y et y->f(x,y) dans K[y] quel que soit x alors f(x,y) est dans K[x,y] ! Ce n'est pas évident au premier abord.

[Nightmare]

Je crois que M. Baire pourrait nous aider !

[Nightmare]

Quelqu'un a une idée? Sans trop d'assurance, je pense avoir réussi à démontrer que c'est vrai dans le cas K=R. Mais pour Q, mes arguments ne marchent plus.

S'il y a des intéressés je posterai ma démarche (qui n'utilise pas Baire contrairement à ce que j'avais suggéré !)

[ffpower]

Salut :we:
Je m'étais moi aussi attaqué à cet exercice il y a quelques temps, ca tombe bien^^

Donc au final, j'ai obtenu que le résultat était vrai si le corps K est indénombrable ( p-e avec la même méthode que toi : j'inverse un Vandermonde ), et que par contre c'est faux si K est dénombrable: Pour obtenir un contrexemple,j énumére les éléments de K par une suite , je note , puis je pose ( qui est bien définie car la somme est en fait finie ).

[Nightmare]

Oui, j'ai bien utilisé Vandermonde :happy3:

Niquel pour le contre exemple

(tu as le don pour clore un topic rapidement :D)