Cette fonction est-elle definie sur C ?
23 messages
- Page 1 sur 2 - 1, 2
cette fonction est-elle definie sur C ?
bonjour
j'ai un souci pour montrer rigoureusement que le fonction F est definie sur C
F(a)=int( exp(-t²/2).exp(-at) dt)
intégral de moins l'infinie a plus l'infinie
avec "a" qui appartient à C.
si vous avez une idée de démonstration merci .. moi je seche.
mathématiquement votre.
j'ai un souci pour montrer rigoureusement que le fonction F est definie sur C
F(a)=int( exp(-t²/2).exp(-at) dt)
intégral de moins l'infinie a plus l'infinie
avec "a" qui appartient à C.
si vous avez une idée de démonstration merci .. moi je seche.
mathématiquement votre.
Sylar a écrit:Peut être peut on commencer par écrire a sous la forme:
a=x+iy ou x,y sont des réels
jy ai pensé bien sur le probleme c'est que c'est une integral a parametre et moi pour le moment je m'interesse au fait quel soit definie ou non et en metant sous la forme x+iy j'ai pas l'impression que sa m'aide beaucoup.
Edrukel a écrit:je pense que le fait de dire qu'on asuffit.
Non ca ne suffit clairement pas.
Si tu mets a sous la forme a=x+iy et utilise ce que dis Sylar, tu peux t'en tirer puisque la valeur absolue d'une intégrale est plus petite que l'intégrale de la valeur absolue.
En calculant l'intégrale de la valeur absolue, on a quelque chose de convergeant en l'infini sans problème.
a+
pourquoi ça ne suffit pas de dire que la limite en +oo et -oo de la fonction est 0 ?
sinon on peut faire ceci qui est rapide quand même et comme ça , pas de travail sur les complexes quand on justifie l'intégrabilité ::
on pose x=t+a ,puis x=rac(2)u (tout ceci , c'est avec la forme canonique)
et on trouve ::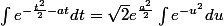
sinon on peut faire ceci qui est rapide quand même et comme ça , pas de travail sur les complexes quand on justifie l'intégrabilité ::
on pose x=t+a ,puis x=rac(2)u (tout ceci , c'est avec la forme canonique)
et on trouve ::
pourquoi se casser la tête ?
=\int_{-\infty}^{+\infty} e^{\frac{-t^2}{2}}e^{-at}dt)
peut s'écrire , pour "a" complexe "pur" :
=\int_{-\infty}^{+\infty} e^{\frac{-t^2}{2}}cos(-at)dt + i \int_{-\infty}^{+\infty} e^{\frac{-t^2}{2}}sin(-at)dt)
et chaqu'une des deux integrales se majorent en valeur absolue par:

qui converge...
on doit pouvoir faire presque pareil avec "a" complexe quelconque...
si a = X+ i Y, on aura en plus une exponentielle en X.t dans l'integrale majorante, ce qui n'est pas genant car c'est l'exponentielle en t^2 qui l'emportera et fera converger l'integrale...
 sera alors l'integrale majorante
sera alors l'integrale majorante
peut s'écrire , pour "a" complexe "pur" :
et chaqu'une des deux integrales se majorent en valeur absolue par:
qui converge...
on doit pouvoir faire presque pareil avec "a" complexe quelconque...
si a = X+ i Y, on aura en plus une exponentielle en X.t dans l'integrale majorante, ce qui n'est pas genant car c'est l'exponentielle en t^2 qui l'emportera et fera converger l'integrale...
cesar a écrit:pourquoi se casser la tête ?
peut s'écrire , pour "a" complexe "pur" :
et chaqu'une des deux integrales se majorent en valeur absolue par:
qui converge...
on doit pouvoir faire presque pareil avec "a" complexe quelconque...
si a = X+ i Y, on aura en plus une exponentielle en X.t dans l'integrale majorante, ce qui n'est pas genant car c'est l'exponentielle en t^2 qui l'emportera et fera converger l'integrale...sera alors l'integrale majorante
donc pour toi il n'y a pas besoin de verifié
-la continuité par rapport au 2 variables à x et a t
-à x fixé f doit etre intégrable sur l'intervalle par rapport à t
-comme tu est sur un ouvert tu dois avoir |f(x,t)|<=g(x,t) avec g continue sur l'intervalle ,intégrale sur cet intervalle et positive sur cet intervalle
il me semble que c un truc comme sa le theoreme des integral a parametre mai je ne suis pas du tous sur...
dans tous les cas merci pour votre interet vous m'aider a avancer..
Edrukel a écrit:pourquoi ça ne suffit pas de dire que la limite en +oo et -oo de la fonction est 0 ?
bonjour
quelle serait la valeur de f(a) définie comme l'intégrale de 1/(x+a) sur R+ ?
a réel strictement positif?
pour faire simple la fonction 1/(x+a) est petite en +infini mais l'aire sous la courbe entre 0 et T elle devient grande quand T->+infini
oui tu as raison, en fait j'avais oublié de voir dans ce mot "intégrabilité" ,le terme de "convergence" :-)
ton exemple n'est pas pour moi :-) je trouve, je sais tout ça
d'ailleurs sur ce problème d'origine exp(-t^2/2-at) je sais qu'il n'ya pas cette situation de ton exemple avec 1/(x+a) :-)
merci encore pour ta réponse
ton exemple n'est pas pour moi :-) je trouve, je sais tout ça
d'ailleurs sur ce problème d'origine exp(-t^2/2-at) je sais qu'il n'ya pas cette situation de ton exemple avec 1/(x+a) :-)
merci encore pour ta réponse
ttoff a écrit:donc pour toi il n'y a pas besoin de verifié
-la continuité par rapport au 2 variables à x et a t
-à x fixé f doit etre intégrable sur l'intervalle par rapport à t
-comme tu est sur un ouvert tu dois avoir |f(x,t)|<=g(x,t) avec g continue sur l'intervalle ,intégrale sur cet intervalle et positive sur cet intervalle
il me semble que c un truc comme sa le theoreme des integral a parametre mai je ne suis pas du tous sur...
dans tous les cas merci pour votre interet vous m'aider a avancer..
Je ne vois pas le rapport.
Je pense que tu mélanges vraiment tout.
On ne demande pas de montrer que la fonction est dérivable ou quoique ce soit, on demande de montrer que pour tout a, elle existe, ce qui est nettement plus faible ...
Edrukel a écrit:ton exemple n'est pas pour moije trouve, je sais tout ça
mais il est pour moi car bien souvent dans des problèmes de limites d'intégrales je regarde simplement le "rectangle d'intégration"
intégrale = Longueur x hauteur
longueur = longueur de l'intervalle d'intégration
hauteur= taille de la fonction
on a des rectangles
-infiniment long de hauteur nulle
- infiniment hauts de longueur nulle
- autres qui ne posent pas de pb
ds les deux premiers cas on regarde ce qui l'emporte et on a répondu à 80% des questions de ce genre.
ça a l'air naïf , ça l'est mais c'est efficace
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
