Certains quadrilatères

[Dacu]

Bonjour!

edit modération : Pourriez vous m'aider à résoudre cet exercice ?

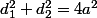
Trouver tous les quadrilatères, sachant que où sont les diagonales et est un côté.
Merci!

[chan79]

Bonjour!
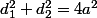
Trouver tous les quadrilatères, sachant que où sont les diagonales et est un côté.
Merci!

Salut
En voilà un.
Il y a aussi tous les losanges.

[Dacu]

Quelles sont les valeurs des côtés et ?
Merci beaucoup!

[chan79]

Quelles sont les valeurs des côtés et ?
Merci beaucoup!

en fonction de quoi ?

[Dacu]

en fonction de quoi ?

En fonction de valeurs ...
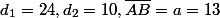
Cordialement!

[chan79]

En fonction de valeurs ...
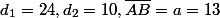
Cordialement!

On ne peut pas répondre; il y a une infinité de figures avec ces hypothèses.
Tu sembles improviser ton énoncé ...

[deltab]

Salut
En voilà un.
Il y a aussi tous les losanges.

En remarquant qu'un triangle, si ce triangle existe, dont 2 côtés sont de longueurs et et le troisième de longueur 2a, est, s'il vérifie la relation est alors un triangle rectangle. Soit AB un segment, de longueur a , C un point du cercle centré en A et de rayon , D un point du cercle centré en B de rayon ., si les 2 segments AC et BD se coupent, ils sont les diagonales du quadrilatère ABCD et l'égalité est alors vérifiée.

[hammana]

Bonjour!

edit modération : Pourriez vous m'aider à résoudre cet exercice ?

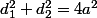
Trouver tous les quadrilatères, sachant que où sont les diagonales et est un côté.
Merci!

Salut

Je propose la solution suivante:
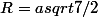
Si AB est le côté de longueur a, I le milieu de AB, C le cercle de centre de AB et de rayon , M un point quelconque de C, tout quadrilatère ayant pour diagonales d1=AM, d2=BM répond à la question (Théorème de la médiane).

[mathafou]

Bonsoir,

C le cercle de centre de AB et de rayon

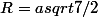
c'est quoi ce truc ???


on choisit (arbitrairement) un segment AB ici = 13 par exemple
on trace le cercle de diamètre AB et on choisit arbitrairement un point M sur ce cercle
on l'a ici choisi de sorte que AM = 5 car alors BM = 12 (13² = 5² + 12²)
soient P et Q les symétriques de A et B par rapport à M (AP = 2AM et BQ = 2BM)
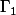
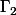
on trace les cercles de centre A de rayon AP et de centre B de rayon BQ
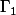
on choisit arbitrairement des points C sur et D sur
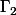
le quadrilatère ABCD satisfait au problème.
on peut se restreindre ou non à des quadrilatères convexes (diagonales se coupant à l'intérieur) ou pas
ce qui donne des infinités de quadrilatères qui conviennent... (4 paramètres arbitraires)

[deltab]

Bonsoir.

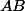
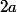
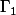
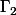
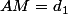
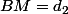
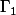
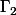
On peut faire un construction analogue à celle faite par Mathafou mais en partant d'un cercle de diamètre de rayon et non de diamètre . Si est un point de , on prendra pour cercles et les cercles centrés en et de rayon et . En choisissant le point sur et le point sur , on aura bien , ie .

Remarque: J'ai repris mon idée initiale en lui ajoutant une construction géométrique, celle-ci est une adaptation de celle proposée par Mathafou mais je ne saurai faire une figure aussi jolie que la sienne.

[mathafou]

Bonjour,

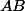
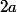
de diamètre de rayon ... on aura bien , ie

tu es sûr ?
si le rayon vaut 2a, le diamètre AB vaudra 4a et ce que tu auras c'est
Mais de toute façon ce que demande l'énoncé ce n'est pas juste une relation "numérique" déconnectée du quadrilatère ABCD, mais que



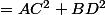
l'énoncé dit bien :
"...et est un côté", pas la moitié d'un côté (voire dans ta construction le quart d'un côté) !!

[deltab]

Bonjour

Bonjour,tu es sûr ?
si le rayon vaut 2a, le diamètre AB vaudra 4a et ce que tu auras c'est
Mais de toute façon ce que demande l'énoncé ce n'est pas juste une relation "numérique" déconnectée du quadrilatère ABCD, mais que



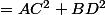
l'énoncé dit bien :
"...et est un côté", pas la moitié d'un côté (voire dans ta construction le quart d'un côté) !!

Désolé, je me suis embrouillé entre la relation à trouver et la longueur a d'un côté.

[siger]

Bonjour,

Pour resumer: il y a une infinté de quadrilateres qui repondent a l'equation d1² + d2² = 4a²
A-
(d1/2)² +(d2/2)² = a²
Il existe donc (comme signalé par Chan79) une infinité de solutions telles que les diagonales soient perpendiculaires (quadrilateres orthogonaux) et qu'elles se coupent en leur milieux
TOUS les losanges et les carres sont donc solutions.
B-
En supposant connu un triplet (d1,d2,a) qui satisfasse l'equation, il existe une infinité de quadrilateres de formes variées qui repondent a la question:
-a partir d'un segment AB = a, on trace 2 cercles de centre A et de rayon d1 et de centre B et de rayon d2.
-b tous les points choisis arbitrairement sur ces cercles conduisent a determiner des quadrilateres repondant a la question.
C-
il existe une infinité de triplets en nombres reels comme (24,10,13) indiqué par chan79, (18,24,15), .....donc une infinité de quadrilateres repondant a la question

[deltab]

Bonjour.

Finalement tout se résume par B) à cause de l'équivalence tout triplet de nombres réels non négatifs vérifiant représente les longueurs des côtés d'un triangle rectangle (éventuellement dégénéré) ABC dont l'hypoténuse AB est de longueur , le somment de l'angle droit est alors sur le cercle de diamètre AB. Dans la construction des quadrilatères faite par Mathafou, le 1er quadrilatère qu'on construit est un losange, c'est le losange ABPQ. Une animation des déplacements des sommets P et Q (un à la fois ou les 2 en même temps sur leurs cercles permettra de visualiser la déformation du losange ABPQ en un quadrilaère.

[deltab]

Bonjour.

Finalement tout se résume par B) à cause de l'équivalence tout triplet de nombres réels non négatifs vérifiant représente les longueurs des côtés d'un triangle rectangle (éventuellement dégénéré) ABC dont l'hypoténuse AB est de longueur , le somment de l'angle droit est alors sur le cercle de diamètre AB. Dans la construction des quadrilatères faite par Mathafou, le 1er quadrilatère qu'on construit est un losange, c'est le losange ABPQ. Une animation des déplacements des sommets P et Q (un à la fois ou les 2 en même temps) sur leurs cercles respectifs permettra de visualiser la déformation du losange ABPQ en un quadrilatère.