Cercles (ex)inscrits

[Pythales]

Bonjour
Trouvé sur un autre forum :

Quelle est l'équation du quatrième degré dont les solutions complexes
I,J1,J2,J3 sont les quatre centres de cercles [ex]inscrits au triangle
A,B,C dont les sommets sont décrits comme solutions complexes d'une équation du troisième degré ?

J'ai pensé à définir les centres des cercles comme barycentre des points A, B et C affectés des coefficients +-a, +-b, +-c (longueurs des côtés), mais j'avoue que je bloque

[catharaxie]

tu peux eclaircir l'enoncé?

ton equation du troisieme degré elle est sur C ou sur R ? ...sur R on tombe sur un triangle isocele ou plat ... ca peut simplifier la chose (trop?)

j'ai du mal a visualiser les 4 cercles exinscrits d'un triangle...tu veux dire exinscrits à deux sommets et au centre de gravité ?

[catharaxie]

j'ai une technique brillante d'inventivité ... tu calcules a la main I, J1, J2 ,J3 et tu multiplies (z-I) (z- J1)( z- J2) ( z-J3)

ou mieux tu les calcules pas et tu balances :

Soient I, J1, J2 J3 les affixes des points considérés,
l'equation recherchée est
(z-I) (z- J1)( z- J2) ( z-J3)


ce post m'interesse mais il y manque un petit quelquechose

[Pythales]

L'énoncé me semblait clair.
Cercle inscrit : intérieur au triangle et tangent à ses 3 côtés. Son centre est évidemment le point de concours des bissectrices intérieures.
Cercles exinscrits : tangents aux 3 côtés du triangle, mais extérieurs au triangle (3 cercles)
Pour être précis : je me donne 3 points d'affixe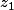 , 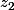et 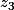, qui définissent un triangle dans le plan complexe. Former l'équation (dans C) du quatrième degré dont les racines sont les affixes des 4 centres. Il semble d'aprés l'énoncé que les coefficients de cette équation puissent s'exprimer en fonction de 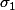, 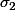et , fonctions symétriques de 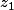, 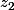et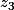
C'est clair ?