Cercle osculateur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AlexisD
- Membre Relatif
- Messages: 168
- Enregistré le: 26 Sep 2009, 15:27
-
 par AlexisD » 02 Nov 2009, 10:24
par AlexisD » 02 Nov 2009, 10:24
Bonjour à tous.
Comment montrer ceci:
On se donne une courbe régulière

paramétrisée par longueur d'arc sur un intervalle I. On suppose qu'en un point

, la courbure
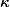
est telle que
 \neq 0)
Comment montrer que le cercle osculateur en
)
coupe la courbe ?
J'avais pensé à poser la fonction:
= \alpha(t) - C(t))
ou C(t) désigne l'équation du cercle osculateur.
Et je voulais montrer que f s'annule au moins une fois. Je pourrais étudier les variations de la fonction,... mais comment utiliser le fait que
 \neq 0)
?
 par alavacommejetepousse » 02 Nov 2009, 10:33
par alavacommejetepousse » 02 Nov 2009, 10:33
bonjour
on écrit l équation du cercle ds le repère local ( M(t0) , f^(p)(t0) , f^(q) (t0) )
-
AlexisD
- Membre Relatif
- Messages: 168
- Enregistré le: 26 Sep 2009, 15:27
-
 par AlexisD » 02 Nov 2009, 10:38
par AlexisD » 02 Nov 2009, 10:38
Mais p est-il ici le plus petit entier de tous les
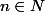
tel que
}(t_o) \neq 0)
ou
}(t_o) \neq 0)
?
-
AlexisD
- Membre Relatif
- Messages: 168
- Enregistré le: 26 Sep 2009, 15:27
-
 par AlexisD » 02 Nov 2009, 15:31
par AlexisD » 02 Nov 2009, 15:31
Je suis navré, mais j'ai un peu de mal encore avec cette proposition, je n'arrive pas à utiliser le fait que
 \neq 0)
-
AlexisD
- Membre Relatif
- Messages: 168
- Enregistré le: 26 Sep 2009, 15:27
-
 par AlexisD » 02 Nov 2009, 15:45
par AlexisD » 02 Nov 2009, 15:45
Et bien, voilà ce que j'écris, mais à l'aveuglette, j'avoue...
= \alpha(t)-C(t)= \alpha(t)-C_o-\frac{1}{\kappa_o}cos(t \kappa_o) T_o-\frac{1}{\kappa_o}sin(t \kappa_o)N_o)
De là, je dérive:
= \alpha'(t)+sin(t \kappa_o)T_o-cos(t \kappa_o)N_o)
Mais quel est le cheminement de la démonstration ?
 par alavacommejetepousse » 02 Nov 2009, 16:11
par alavacommejetepousse » 02 Nov 2009, 16:11
on a un point birégulier pour simplifier je prends s0= 0
ds le repère (M(0),t,n) l'équation du cercle est
X^2 +Y^2 -2RY= 0
la fonction
f(s) = X^2(s) +Y^2(s) -2RY(s) s'annule en 0 ainsi que ses deux premières dérivées mais pas sa dérivée troisième ce qui prouve qu'elle change de signe au voisinage de 0
-
AlexisD
- Membre Relatif
- Messages: 168
- Enregistré le: 26 Sep 2009, 15:27
-
 par AlexisD » 02 Nov 2009, 16:26
par AlexisD » 02 Nov 2009, 16:26
Ah oui...
pour la première derivée, je vois car c'est en fait le vecteur tangent de pente nulle, donc c'est 0
Mais pour la dérivée seconde qui est égale à K. N(o), pourquoi est-ce nul ?
-
AlexisD
- Membre Relatif
- Messages: 168
- Enregistré le: 26 Sep 2009, 15:27
-
 par AlexisD » 02 Nov 2009, 16:44
par AlexisD » 02 Nov 2009, 16:44
OK bien merci.
Je ne suis pas très à l'aise avec ce genre d'exercice qui en fait n'est pas si compliqué; je n'ai pas le coup d'oeil géométrique, c'est dommage.
Cela dit j'ai parfaitement compris la démonstration de la proposition. Merci bien.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
