Centre d'un certain groupe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
par chombier » 27 Aoû 2015, 18:09
J'ai des petits soucis avec ce problème :
Soit
)
un groupe et
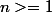
un entier fixé, tel que l'application
soit un automorphisme.
Prouver que :
)
L'application x->x^n est une bijection donc :
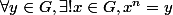
C'est un morphisme donc :
^n = x^n y^n)
Il faut démontrer que :
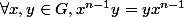
Heureusement j'ai la solution ! Mais je ne la comprends pas :
Soient x, y deux élément quelconques de G.
De
^n = x^n y^n)
, on déduit que
^{n-1} = x^{n-1}y^{n-1})
Je n'en met pas plus car je ne vois pas du tout comment passer d'une affirmation à l'autre.
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 27 Aoû 2015, 18:15
salut
si G n'est pas abélien alors
^n \ne x^ny^n)
mais
^n = xyxyxy...xy)
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Robot
par Robot » 27 Aoû 2015, 18:16
Il suffit de multiplier par
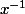
à gauche et
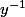
à droite.
-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
par chombier » 27 Aoû 2015, 18:18
Oui, ça doit être classique, il faut utiliser le fait que
^n = x (yx)^{n-1} y)
Classique quand on a rencontré le cas deux ou trois fois.
Ca m'est encore assez étranger :-/
^{n-1} = x^{-1} (xy)^{n} y^{-1})
^{n-1} = x^{-1} x^n y^n y^{-1})
(car x->x^n est un morphisme)
^{n-1} = x^{n-1} y^{n-1})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
