Cauchy-Schwarz
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 16 Fév 2010, 16:07
par jeje56 » 16 Fév 2010, 16:07
Bonjour,
Soit f C1 par morceaux, 2pi périodique, de coefficient de Fourier complexe c_n ; je dois montrer la convergence de la série
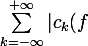|)
Pour cela on utilise l'inégalité de Cauchy-Schwarz :
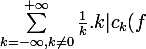|\leq \sqrt{\sum_{k=-\infty,k\neq 0}^{+\infty}\frac{1}{k^2}}\sqrt{\sum_{k=-\infty}^{+\infty}k^2|c_k(f)|^2})
Qu'est ce qui justifie ici l'utilisation de cette formule ?
Merci !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Fév 2010, 16:23
par Nightmare » 16 Fév 2010, 16:23
Salut,
on peut utiliser Cauchy-Schwartz pour une somme finie puis passer à la limite.
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 16 Fév 2010, 17:17
par jeje56 » 16 Fév 2010, 17:17
D'accord, mais dans ce cas, il y a un rapport avec un produit scalaire ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités