Bonsoir,
Je suis face à un problème assez compliqué pour ma part. Comme certains s'en souviennent (cf d'autres posts), c'est issu d'un sujet en anglais.
Supposons une séquence de fonctions continues
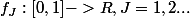
qui converge vers une fonction continue f. On utilise

pour définir le domaine variable de la fonction.
Par exemple, pour J=1 on écrit :
=t)
Considérons les points dyadiques suivants associés à la fonction
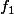
:
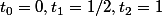
et l'ensemble
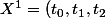)
et la partition de [0,1[ en deux sous intervalles
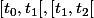
.
On note que
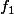
est une fonction linéaire sur chacun de ces sous-intervalles et donc linéaire sur [0,1].
Plus généralement, pour J>1, on définit:
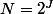
, et le sous-ensemble:
=(0,2^{-J},2*2^{-J},3*2^{-J},...,1))
On note aussi
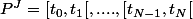
L'ensemble des points dyadiques est
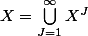
qui est dense sur [0,1].
On constate les points suivants :
1)
 = f_{J}(t))
pour tous les
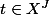
. De ce fait la valeur de
)
ne change jamais au point dyadique
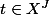
quand J' augmente.
2)
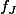
est continue pour tous les J et linéaire sur chaque sous intervalle
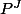
3)
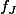
converges uniformément vers une fonction continue
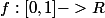
quand J tend vers l'infini.
Pour définir
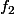
, on sait que
=f_{1}(t))
au point
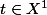
et on modifie les valeurs dans
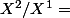
{ 1/4 , 1/8 }. On trouve :
 = f_{1} (1/4)-1/\sqrt8 = [f_{1} (1/2) + f_{1} (1) ] / 2 - 1/\sqrt8 = -0.1036)
De même
 = 1.1036)
On étend le procédé et on obtient :
Pour
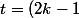 2^{-(J+1)} \in X^{J+1}/X^J , k=1,...,2^J)
et on définit
 = f_{J}(t) + (-1)^{k+J} 2^{-J/2-1})
Nous souhaiterions analyser la convergence de
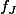
vers f. Il faut se rappeler que l'espace des fonctions continues de [0,1] à R , noté
)
est un espace de Banach:
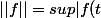 |)
pour
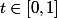
Question 1: Prouvez que la séquence
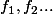
converge uniformément vers une fonction continue
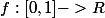
en montrant qu'il s'agit d'une séquence de Cauchy
En fait, si je comprends bien, on partitionne une fonction linéaire sur [0,1] et plus notre J augmente, plus on obtient une fonction qui oscille sur [0,1]. On finit par obtenir une fonction en "dents de scie" que je suppose continue partout, mais dérivable nul part
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
